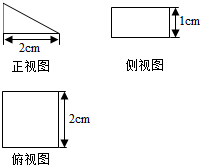
题目内容
19．把一个大金属球表面涂漆，共需油漆2.4公斤．若把这个大金属球熔化制成64个大小都相同的小金属球，不计损耗，将这些小金属球表面都涂漆，需要用漆9.6公斤．分析 设大金属球的半径为R，小金属球的半径为r，根据体积相等建立等式关系，然后求出64个小球球面的总面积，从而求出所求．
解答 解：设大金属球的半径为R，小金属球的半径为r，依题意得知：面积为4πR2需要要用油漆2.4kg．
由$\frac{4}{3}π{R}^{3}$=64×$\frac{4}{3}π{r}^{3}$，可得r=$\frac{1}{4}$R
64个小球球面的总面积为：64×4πr2=4×（4πR2）
∴4×2.4=9.6（kg）
故答案为：9.6．
点评 本题是基础题，考查球的体积的求法，考查计算能力，送分题．
练习册系列答案
阅读快车系列答案
相关题目
14．设集合A={x|x2-9＜0}，B={x|-1＜x≤5}，则A∩B=（ ）
| A． | （-3，-1） | B． | （-3，5] | C． | （3，5] | D． | （-1，3） |
4．在复平面内，复数$\frac{2+i}{1-i}$（i是虚数单位）对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
8．
已知某路口最高限速50km/h，电子监控测得连续6辆汽车的速度如图的茎叶图（单位：km/h）．若从中任取2辆，则恰好有1辆汽车超速的概率为（ ）
已知某路口最高限速50km/h，电子监控测得连续6辆汽车的速度如图的茎叶图（单位：km/h）．若从中任取2辆，则恰好有1辆汽车超速的概率为（ ）| A． | $\frac{4}{15}$ | B． | $\frac{2}{5}$ | C． | $\frac{8}{15}$ | D． | $\frac{3}{5}$ |