Question

（2007•揭阳二模）如图，线段AB过y轴负半轴上一点M（0，a），A、B两点到y轴距离的差为2k．
（Ⅰ）若AB所在的直线的斜率为k（k≠0），求以y轴为对称轴，且过A、O、B三点的抛物线的方程；
（Ⅱ）设（1）中所确定的抛物线为C，点M是C的焦点，若直线AB的倾斜角为60°，又点P在抛物线C上由A到B运动，试求△PAB面积的最大值．

Answer 1

分析：（1）依题意设所求的抛物线方程为x²=-2py（p＞0），直线AB的方程为y=kx+a，由

y=kx+a x2=-2py

得x²+2pkx+2pa=0
设A（x₁，y₁），B（x₂，y₂）（x₁＜0，x₂＞0，y₁＜0，y₂＜0），x₁+x₂=-2pk，若|x₁|-|x₂|=2k可求p
（2）解法1：可得直线AB的方程为y=

3

x-

1

2

，解方程组

x2=-2y y= 3 x- 1 2

可求点A，B，从而可求AB，设点P（m，n），依题意知-

3

-2≤m≤-

3

+2，且n=-

1

2

m2，根据点P到直线AB的距离d=

| 3 m-n- 1 2 |

2

=

| 1 2 m2+ 3 m- 1 2 |

2

可求面积的最大值
解法2：直线AB的方程为y=

3

x-

1

2

，由

x2=-2y y= 3 x- 1 2

得x2+2

3

x-1=0，x1+x2=-2

3

，x₁x₂=-1，
|AB|=

1+k2

|x1-x2|=2

(x1+x2)2-4x1x2

以下同法一

解答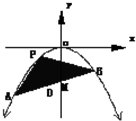：（1）解：依题意设所求的抛物线方程为x²=-2py（p＞0），----------（1分）
∵直线AB的斜率为k且过点M（0，a）∴直线AB的方程为y=kx+a
由

y=kx+a x2=-2py

得x²+2pkx+2pa=0----------①------------------（3分）
设A（x₁，y₁），B（x₂，y₂）（x₁＜0，x₂＞0，y₁＜0，y₂＜0）
则x₁，x₂是方程①的两个实根
∴x₁+x₂=-2pk，若|x₁|-|x₂|=2k
则-x₁-x₂=2k，-2pk=-2k∴p=1---------------------------（5分）
若|x₂|-|x₁|=2k则x₁+x₂=-2pk=2k∴p=-1与p＞0矛盾----（6分）
∴该抛物线的方程为x²=-2y．-------（7分）
（2）解法1：抛物线x²=-2y的焦点为（0，-

1

2

）即M点坐标为（0，-

1

2

）
直线AB的斜率k=tan60°=

3

∴直线AB的方程为y=

3

x-

1

2

，-----------------（8分）
解方程组

x2=-2y y= 3 x- 1 2

得

x1=- 3 -2 y1=- 7+4 3 2

x2=- 3 +2 y2=- 7-4 3 2

即点A(-

3

-2，-

7+4 3

2

)，B(-

3

+2，-

7-4 3

2

)-------------------（10分）
∴|AB|=

42+(4 3 )2

=8
设点P（m，n），依题意知-

3

-2≤m≤-

3

+2，且n=-

1

2

m2
则点P到直线AB的距离d=

| 3 m-n- 1 2 |

2

=

| 1 2 m2+ 3 m- 1 2 |

2

=

|-(m+ 3 )2+4|

4

当m=-

3

时，d_max=1，--------------------------------（13分）
这时Smax=

1

2

|AB|dmax=

1

2

×8×1=4．-----------------------（15分）
解法2：抛物线x²=-2y的焦点为（0，-

1

2

）即M点坐标为（0，-

1

2

）
直线AB的斜率k=tan60°=

3

∴直线AB的方程为y=

3

x-

1

2

，
由

x2=-2y y= 3 x- 1 2

得x2+2

3

x-1=0∴x1+x2=-2

3

，x₁x₂=-1，
∴|AB|=

1+k2

|x1-x2|=2

(x1+x2)2-4x1x2

=2

12+4

=8[以下同上]

点评：本题主要考查了利用抛物线的性质求解抛物线的方程，直线与抛物线的位置关系的应用，点到直线的距离公式的应用，利用二次函数的性质求解函数的最值等知识的综合应用，要注意方程的思想的应用．