题目内容
直线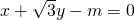 与圆x2+y2=1在第一象限内有两个不同的交点,则m的范围
与圆x2+y2=1在第一象限内有两个不同的交点,则m的范围
- A.1<m<2
- B.
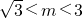
- C.
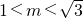
- D.
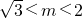
D
分析:由直线的倾斜角以及它在y轴上的截距,结合条件判断 m>0,求出直线和圆相切时的m值,再求出直线过点(0,1)
时的m值,从而可求得m的范围.
解答:由于直线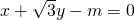 ,即 y=-
,即 y=- x+
x+ m,它的斜率等于-
m,它的斜率等于- ,故它的倾斜角等于150°,
,故它的倾斜角等于150°,
且直线在y轴上的截距等于 m.
m.
由于直线与圆x2+y2=1在第一象限内有两个不同的交点,故有 m>0,即 m>0.
m>0,即 m>0.
当直线和圆相切时,由r=1=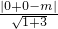 ,解得 m=2.
,解得 m=2.
当直线过圆和y轴的交点(0,1)时,由1=0+ ×1-m=0,可得 m=
×1-m=0,可得 m= .
.
数形结合可得,满足条件的m的范围为( ,2 ),
,2 ),
故选 D.

点评:本题主要考查了直线与圆相交的综合问题,注意考虑直线与圆相切、直线过圆和y轴的交点(0,1)这两种特殊情况,
体现了分类讨论的数学思想,属于中档题.
分析:由直线的倾斜角以及它在y轴上的截距,结合条件判断 m>0,求出直线和圆相切时的m值,再求出直线过点(0,1)
时的m值,从而可求得m的范围.
解答:由于直线
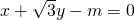 ,即 y=-
,即 y=- x+
x+ m,它的斜率等于-
m,它的斜率等于- ,故它的倾斜角等于150°,
,故它的倾斜角等于150°,且直线在y轴上的截距等于
 m.
m.由于直线与圆x2+y2=1在第一象限内有两个不同的交点,故有
 m>0,即 m>0.
m>0,即 m>0.当直线和圆相切时,由r=1=
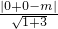 ,解得 m=2.
,解得 m=2.当直线过圆和y轴的交点(0,1)时,由1=0+
 ×1-m=0,可得 m=
×1-m=0,可得 m= .
.数形结合可得,满足条件的m的范围为(
 ,2 ),
,2 ),故选 D.

点评:本题主要考查了直线与圆相交的综合问题,注意考虑直线与圆相切、直线过圆和y轴的交点(0,1)这两种特殊情况,
体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目