题目内容
过原点的直线与圆x2+y2+4x+3=0相切，若切点在第三象限，则该直线的方程是
y=
x
| ||
| 3 |
y=
x
．
| ||
| 3 |
分析：画出图形，利用三角函数可以求直线的斜率，求出直线方程．
解答：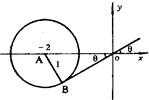
解：如图，圆方程为（x+2）2+y2=1，圆心为A（-2，0），半径为1，
∴sinθ=
，θ=
，tanθ=
．
切线方程为：y=
x
故答案为：y=
x
解：如图，圆方程为（x+2）2+y2=1，圆心为A（-2，0），半径为1，∴sinθ=
| 1 |
| 2 |
| π |
| 6 |
| ||
| 3 |
切线方程为：y=
| ||
| 3 |
故答案为：y=
| ||
| 3 |
点评：本题考查直线和方程的应用，数形结合的数学思想，是基础题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
过原点的直线与圆x2+y2+4x+3=0相切，若切点在第三象限，则该直线的方程是（ ）
A、y=
| ||||
B、y=-
| ||||
C、y=
| ||||
D、y=-
|