题目内容
已知Pn是把Pn-1Pn+1线段作n等分的分点中最靠近Pn+1的点,设线段P1P2,P2P3,…,PnPn+1,的长度分别为a1,a2,a3,…,an,其中a1=1.
(1)写出a2,a3和an的表达式;
(2)证明a1+a2+a3+…+an<3;
(3)设点Mn(n,an),在这些点中是否存在两个点同时在函数
 )的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.
)的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.
【答案】分析:(1)由于Pn是把Pn-1Pn+1线段作n等分的分点中最靠近Pn+1的点,所以知Pn-1Pn=(n-1)PnPn-1,从而可得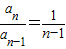 ,进而利用叠乘即可求出a2,a3和an的表达式;
,进而利用叠乘即可求出a2,a3和an的表达式;
(2)对通项进行放缩,再求和,利用等比数列的求和公式即可证明;
(3)假设存在,即可得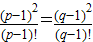 ,再证明数列
,再证明数列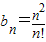 的单调减即可.
的单调减即可.
解答:解:(1)由已知Pn-1Pn=(n-1)PnPn-1
令n=2,P1P2=P2P3,∴a2=1,同理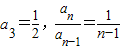
∴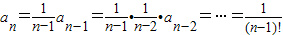
(2)∵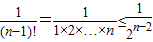
∴a1+a2+a3+…+an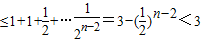
而n=1时,结论成立,故a1+a2+a3+…+an<3;
(3)假设有两个点A(p,ap),B(q,aq),都在函数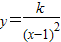 上,即
上,即 ,
,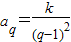
所以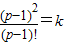 ,
,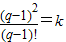 ,消去k得
,消去k得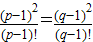 ①,以下考查数列
①,以下考查数列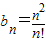 的增减情况,
的增减情况,
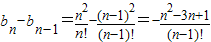 ,
,
当n>2时,n2-3n+1>0,所以对于数列{bn}为递减数列
∴不可能存在p,q使得①式成立,因而不存在.
点评:本题以线段为载体,考查数列的通项,考查放缩法的运用,考查函数的单调性,综合性强.
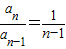 ,进而利用叠乘即可求出a2,a3和an的表达式;
,进而利用叠乘即可求出a2,a3和an的表达式;(2)对通项进行放缩,再求和,利用等比数列的求和公式即可证明;
(3)假设存在,即可得
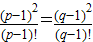 ,再证明数列
,再证明数列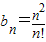 的单调减即可.
的单调减即可.解答:解:(1)由已知Pn-1Pn=(n-1)PnPn-1
令n=2,P1P2=P2P3,∴a2=1,同理
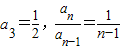
∴
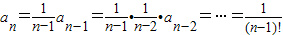
(2)∵
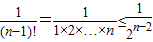
∴a1+a2+a3+…+an
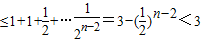
而n=1时,结论成立,故a1+a2+a3+…+an<3;
(3)假设有两个点A(p,ap),B(q,aq),都在函数
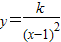 上,即
上,即 ,
,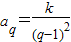
所以
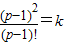 ,
,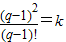 ,消去k得
,消去k得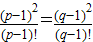 ①,以下考查数列
①,以下考查数列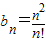 的增减情况,
的增减情况,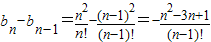 ,
,当n>2时,n2-3n+1>0,所以对于数列{bn}为递减数列
∴不可能存在p,q使得①式成立,因而不存在.
点评:本题以线段为载体,考查数列的通项,考查放缩法的运用,考查函数的单调性,综合性强.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
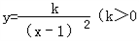 )的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由。
)的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由。