题目内容
已知AB是椭圆
+
=1的长轴,若把该长轴n等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点P1,P2,…,Pn-1,设左焦点为F1,则
(|F1A|+|F1P1|+…+|F1Pn-1|+|F1B|)=
| x2 |
| 4 |
| y2 |
| 3 |
| lim |
| n→∞ |
| 1 |
| n |
2
2
.分析:由椭圆的定义可得|F1Pi|+|F2Pi|=2a=4,由此求得|F1P1|+…+|F1Pn-1|的值,而|F1A|+|F1B|=2a=4,从而求得|F1A|+|F1P1|+…+|F1Pn-1|+|F1B|的值,代入要求的式子求出结果.
解答:解:设右焦点为F2,由椭圆的定义可得|F1Pi|+|F2Pi|=2a=4,
由题意知 点P1,P2,…,Pn-1 关于y轴成对称分布,
∴|F1P1|+…+|F1Pn-1|=
(|F1Pi|)=
(|F1Pi|+|F2Pi|)=(n-2)•a=2(n-2),
而|F1A|+|F1B|=2a=4,
故|F1A|+|F1P1|+…+|F1Pn-1|+|F1B|=2n-4+4=2n,
∴
(|F1A|+|F1P1|+…+|F1Pn-1|+|F1B|)=
(2n)=2,
故答案为:2.
由题意知 点P1,P2,…,Pn-1 关于y轴成对称分布,
∴|F1P1|+…+|F1Pn-1|=
| n-2 |
 |
| i=1 |
| 1 |
| 2 |
| n-2 |
 |
| i=1 |
而|F1A|+|F1B|=2a=4,
故|F1A|+|F1P1|+…+|F1Pn-1|+|F1B|=2n-4+4=2n,
∴
| lim |
| n→∞ |
| 1 |
| n |
| lim |
| n→∞ |
| 1 |
| n |
故答案为:2.
点评:本题考查椭圆的定义、标准方程,以及简单性质的应用,求数列的极限,求出故|F1A|+|F1P1|+…+|F1Pn-1|+|F1B|=2n 是解题的关键和难点,属于难题.

练习册系列答案
相关题目
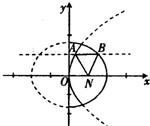 已知定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆
已知定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆