题目内容
(本题满分14分)已知函数 (
( ,实数
,实数 ,
, 为常数).
为常数).
(Ⅰ)若 ,求函数
,求函数 的极值;
的极值;
(Ⅱ)若 ,讨论函数
,讨论函数 的单
的单 调性.
调性.
 (
( ,实数
,实数 ,
, 为常数).
为常数).(Ⅰ)若
 ,求函数
,求函数 的极值;
的极值;(Ⅱ)若
 ,讨论函数
,讨论函数 的单
的单 调性.
调性.解:
(Ⅰ)
 在
在 处取得极小值
处取得极小值 .
.
(Ⅱ)当 ,即
,即 时,函数
时,函数 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 ,即
,即 时,函数
时,函数
 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 ;
;
当 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ;
;
当 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 .…………………
.…………………
(Ⅰ)

 在
在 处取得极小值
处取得极小值 .
. (Ⅱ)当
 ,即
,即 时,函数
时,函数 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;当
 ,即
,即 时,函数
时,函数
 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 ;
;当
 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ;
;当
 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 .…………………
.…………………解:(Ⅰ) 函数
函数 ,则
,则 ,…………………1分
,…………………1分
令 ,得
,得 (舍去),
(舍去), . ………………
. ……………… …………………………2分
…………………………2分
当 时,
时, ,函数单调递减;………………
,函数单调递减;……………… …………………………3分
…………………………3分
当 时,
时, ,函数单调递增;……
,函数单调递增;…… ……………………………………4分
……………………………………4分
∴ 在
在 处取得极小值
处取得极小值 . ……………………………………5分
. ……………………………………5分
(Ⅱ)由于 ,则
,则 ,从而
,从而 ,
, 则
则
 …………………………………………6分
…………………………………………6分
令
 ,得
,得 ,
,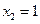 . ……
. …… …
…
 ……………………
…………………… …………7分
…………7分
① 当 ,即
,即 时,函数
时,函数 的单调递减区间为
的单调递减区间为
 ,单调递增区间为
,单调递增区间为 ;8分
;8分
② 当 ,即
,即 时,列表如下
时,列表如下 :
:
所以,函数 的单调递增区间为
的单调递增区间为
 ,
, ,单调递减区间为
,单调递减区间为 ;…………10分
;…………10分
当 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ;……………11分
;……………11分
③ 当 ,即
,即 时,列表如下:
时,列表如下:
所以函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 ; ……………13分
; ……………13分
综上:当 ,即
,即 时,函数
时,函数 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 ,即
,即 时,函数
时,函数
 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 ;
;
当 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ;
;
当 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 .…………………………14分
.…………………………14分
 函数
函数 ,则
,则 ,…………………1分
,…………………1分令
 ,得
,得 (舍去),
(舍去), . ………………
. ……………… …………………………2分
…………………………2分当
 时,
时, ,函数单调递减;………………
,函数单调递减;……………… …………………………3分
…………………………3分当
 时,
时, ,函数单调递增;……
,函数单调递增;…… ……………………………………4分
……………………………………4分∴
 在
在 处取得极小值
处取得极小值 . ……………………………………5分
. ……………………………………5分(Ⅱ)由于
 ,则
,则 ,从而
,从而 ,
, 则
则 …………………………………………6分
…………………………………………6分令

 ,得
,得 ,
,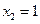 . ……
. …… …
…
 ……………………
…………………… …………7分
…………7分① 当
 ,即
,即 时,函数
时,函数 的单调递减区间为
的单调递减区间为
 ,单调递增区间为
,单调递增区间为 ;8分
;8分② 当
 ,即
,即 时,列表如下
时,列表如下 :
: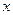 |  |  |  |
 |  |  |  |
 |  |  |  |
 的单调递增区间为
的单调递增区间为
 ,
, ,单调递减区间为
,单调递减区间为 ;…………10分
;…………10分当
 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ;……………11分
;……………11分③ 当
 ,即
,即 时,列表如下:
时,列表如下: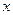 |  |  |  |
 |  |  |   |
 |  |  |  |
 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 ; ……………13分
; ……………13分综上:当
 ,即
,即 时,函数
时,函数 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;当
 ,即
,即 时,函数
时,函数
 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 ;
;当
 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ;
;当
 ,即
,即 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 .…………………………14分
.…………………………14分
练习册系列答案
相关题目
 满足
满足 ,则
,则


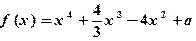
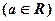
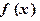 的极大值;
的极大值;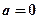 时,求函数
时,求函数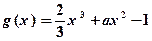 ,当
,当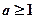 时,
时,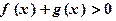 恒成立,求
恒成立,求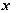 的取值范围.
的取值范围.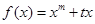 的导数
的导数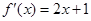 ,则数列
,则数列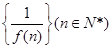 的前n项
的前n项
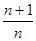


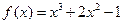 ,则
,则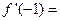 ( )。
( )。 



 ( )
( ) 内均有零点
内均有零点
 内有零点,在区间
内有零点,在区间 内无零点
内无零点
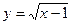 ,则它的导函数是 ( )
,则它的导函数是 ( )



 的解析式可能是( )
的解析式可能是( )


