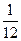题目内容
关于x的方程
+a=x有两个不相等的实数根,则实数a的取值范围是______.
| 1-x2 |
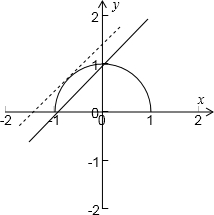
原方程的解可以视为函数y=x-a(y≥0)与函数y=
的图象的交点的横坐标.
函数y=
的图象是半圆y2=1-x2(y≥0),如图所示,
当直线与圆相切时,
=1,∴a=-
(正值舍去)
利用平行直线系y=x-a(y≥0)与函数y=
的图象有两个不同的交点,可得实数a的取值范围是(-
,-1]
故答案为:(-
,-1]
| 1-x2 |
函数y=
| 1-x2 |
当直线与圆相切时,
| |a| | ||
|
| 2 |
利用平行直线系y=x-a(y≥0)与函数y=
| 1-x2 |
| 2 |
故答案为:(-
| 2 |


练习册系列答案
相关题目
 ,其中x是校服的月产量,问:(1)将利润表示为关于月产量x的函数
,其中x是校服的月产量,问:(1)将利润表示为关于月产量x的函数 .(2)当月产量为何值时,工厂所获利润最大?最大利润为多少元?(总收益=总成本+利润)
.(2)当月产量为何值时,工厂所获利润最大?最大利润为多少元?(总收益=总成本+利润)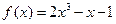 零点的个数为 ( )
零点的个数为 ( )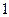
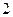
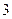
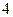
 ,若关于
,若关于 的方程
的方程 恰有5个不同的实数解
恰有5个不同的实数解 ,则
,则 ( )
( )