题目内容
一个口袋内装有大小相同且已编有不同号码的4个黑球和3个红球，某人一次从中摸出2个球。
（1）如果摸到球中含有红球就中奖， 那么此人中奖的概率是多少？
（2）如果摸到的两个球都时红球，那么就中大奖，在有放回的3次摸球中，此人恰好两次中大奖的概率是多少？
【答案】
（1）记“从袋中摸出的两个球中含有红球”为事件A，
则P（B）=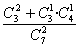
=
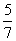．（或“不含红球即摸出的两个球都是黑球”为事件）
．
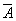∵P（）=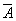
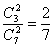．∴P（A）=-1-P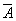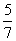（）=． 答：此人中奖的概率是
．
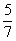（2）记从“袋中摸出的两个球都是红球”为事件B，则P（B）＝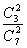
＝
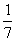． 由于有放回的3次摸，每次是否摸到两个红球之间没有影响．所以3次摸球恰好有两次中大奖相当于作3次独立重复试验，根据n次独立重复试验中事件恰好发生k次的概率公式得， P3（2）＝C23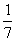（）2·（1-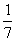）3-2=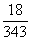
．答：此人恰好两倍欠中大奖的概率是．
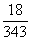练习册系列答案
相关题目