题目内容
已知中心在原点,焦点在 轴上的椭圆,离心率
轴上的椭圆,离心率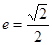 ,且经过抛物线
,且经过抛物线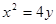 的焦点.
的焦点.
(1)求椭圆的标准方程;
(2)若过点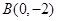 的直线
的直线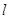 (斜率不等于零)与椭圆交于不同的两点
(斜率不等于零)与椭圆交于不同的两点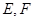 (
(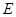 在
在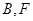
之间),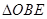 与
与 面积之比为
面积之比为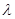 ,求
,求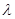 的取值范围.
的取值范围.
【答案】
解:(1)设椭圆的方程为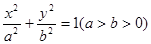 ,则
,则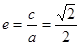 ①,
①,
∵抛物线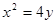 的焦点为(0, 1), ….2分
的焦点为(0, 1), ….2分
∴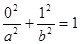 ②
②
由①②解得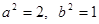 . ……4分
. ……4分
∴椭圆的标准方程为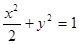 . ……5分
. ……5分
(2)如图,由题意知 的斜率存在且不为零,
的斜率存在且不为零,
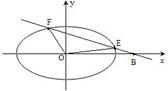
设 方程为
方程为 ③,
③,
将③代入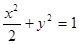 ,整理,得
,整理,得
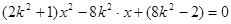 ,由
,由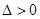 得
得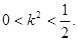 ……7分
……7分
设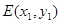 、
、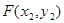 ,则
,则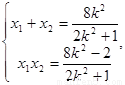 ④
④
令 ,
则
,
则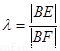 ,……9分
,……9分
由此可得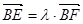 ,
,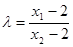 ,且
,且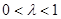 .由④知
.由④知 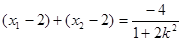 ,
,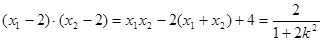 .
.
∴ 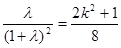 , 即
, 即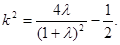 ……12分
……12分
∵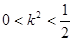 ,∴
,∴
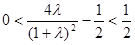 ,解得
,解得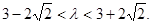
又∵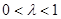 , ∴
, ∴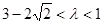 ,……13分
,……13分
∴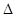 OBE与
OBE与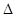 OBF面积之比的取值范围是(
OBF面积之比的取值范围是(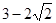 , 1). ……14分
, 1). ……14分
【解析】略

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
