题目内容
已知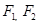 为椭圆
为椭圆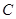 :
: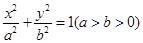 的左、右焦点,过椭圆右焦点F2斜率为
的左、右焦点,过椭圆右焦点F2斜率为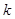 (
(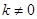 )的直线
)的直线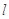 与椭圆
与椭圆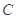 相交于
相交于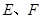 两点,
两点,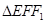 的周长为8,且椭圆C与圆
的周长为8,且椭圆C与圆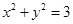 相切。
相切。
(1)求椭圆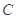 的方程;
的方程;
(2)设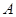 为椭圆的右顶点,直线
为椭圆的右顶点,直线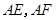 分别交直线
分别交直线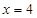 于点
于点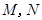 ,线段
,线段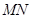 的中点为
的中点为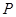 ,记直线
,记直线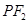 的斜率为
的斜率为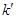 ,求证
,求证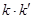 为定值.
为定值.
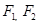 为椭圆
为椭圆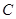 :
: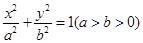 的左、右焦点,过椭圆右焦点F2斜率为
的左、右焦点,过椭圆右焦点F2斜率为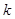 (
(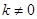 )的直线
)的直线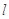 与椭圆
与椭圆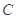 相交于
相交于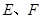 两点,
两点,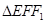 的周长为8,且椭圆C与圆
的周长为8,且椭圆C与圆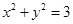 相切。
相切。(1)求椭圆
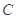 的方程;
的方程;(2)设
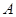 为椭圆的右顶点,直线
为椭圆的右顶点,直线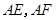 分别交直线
分别交直线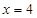 于点
于点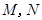 ,线段
,线段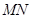 的中点为
的中点为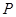 ,记直线
,记直线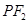 的斜率为
的斜率为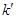 ,求证
,求证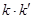 为定值.
为定值.(1)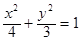 (2)
(2)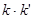 =
=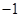 证明详见解析.
证明详见解析.
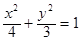 (2)
(2)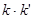 =
=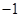 证明详见解析.
证明详见解析.试题分析:(1)由
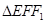 的周长为8,可得4a=8,又由椭圆C与圆
的周长为8,可得4a=8,又由椭圆C与圆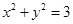 相切,可得b2=3,即可求得椭圆
相切,可得b2=3,即可求得椭圆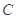 的方程为
的方程为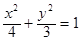 .
.(2)设过点
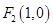 的直线
的直线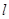 方程为:
方程为: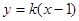 ,设点
,设点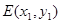 ,点
,点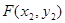 ,将直线
,将直线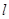 方程
方程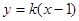 代入椭圆
代入椭圆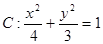 中,整理可得关于x的一元二次方程,该方程由两个不等的实数根,其判别式恒大于零,求出
中,整理可得关于x的一元二次方程,该方程由两个不等的实数根,其判别式恒大于零,求出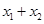 ,
,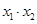 的表达式,由点斜式分别写出直线AE,AF的方程,然后求出点M,N的坐标,在求出点P的坐标,由两点的斜率公式求出直线
的表达式,由点斜式分别写出直线AE,AF的方程,然后求出点M,N的坐标,在求出点P的坐标,由两点的斜率公式求出直线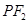 的斜率
的斜率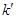 ,整理即可求得
,整理即可求得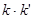 =
=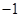 .
.(1)由题意得
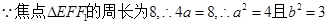 3分
3分所求椭圆C的方程为
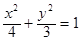 . 4分
. 4分(2)设过点
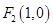 的直线
的直线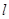 方程为:
方程为: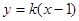 ,
,设点
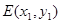 ,点
,点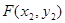 5分
5分将直线
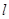 方程
方程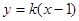 代入椭圆
代入椭圆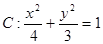
整理得:
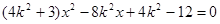 6分
6分因为点
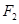 在椭圆内,所以直线
在椭圆内,所以直线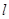 和椭圆都相交,
和椭圆都相交,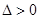 恒成立,
恒成立,且
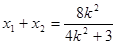
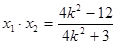 7分
7分直线
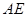 的方程为:
的方程为: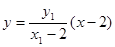 ,直线
,直线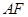 的方程为:
的方程为: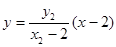
令
 ,得点
,得点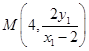 ,
,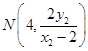 ,
,所以点
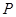 的坐标
的坐标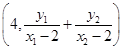 9分
9分直线
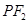 的斜率为
的斜率为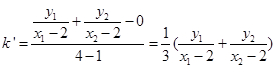
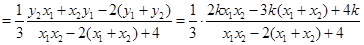 11分
11分将
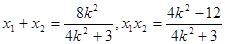 代入上式得:
代入上式得: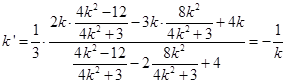
所以
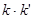 为定值
为定值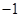

练习册系列答案
相关题目
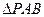 所在的平面
所在的平面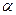 和四边形
和四边形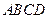 所在的平面
所在的平面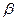 垂直,且
垂直,且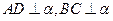 ,
,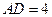 ,
,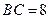 ,
,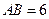 ,
,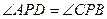 ,则点
,则点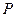 在平面
在平面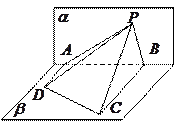
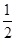 ,m)共线,则实数m=________.
,m)共线,则实数m=________.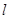 的参数方程为
的参数方程为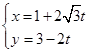 (
(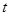 为参数),则直线
为参数),则直线


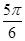
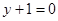 的倾斜角
的倾斜角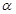 的大小是___ __.
的大小是___ __.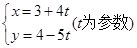 的斜率为______________________。
的斜率为______________________。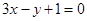 的斜率是( )
的斜率是( )



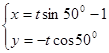 (t为参数),则直线的倾斜角为( )
(t为参数),则直线的倾斜角为( )