题目内容
已知倾斜角为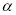 的直线
的直线 过
过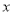 轴上一点
轴上一点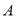 (非坐标原点
(非坐标原点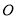 ),直线
),直线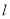 上有一点
上有一点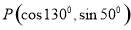 ,且
,且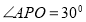 ,则
,则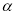 等于( )
等于( )
A.100° B.160° C.100°或160° D.130°
练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
题目内容
已知倾斜角为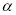 的直线
的直线 过
过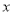 轴上一点
轴上一点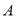 (非坐标原点
(非坐标原点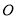 ),直线
),直线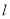 上有一点
上有一点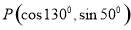 ,且
,且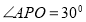 ,则
,则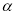 等于( )
等于( )
A.100° B.160° C.100°或160° D.130°
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案