题目内容
已知椭圆P的中心O在坐标原点,焦点在x坐标轴上,且经过点A(0,2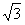 ),离心率为
),离心率为 。
。
(1)求椭圆P的方程;
(2)是否存在过点E(0,-4)的直线l交椭圆P于点R,T,且满足 ,若存在,求直线l的方程;若不存在,请说明理由。
,若存在,求直线l的方程;若不存在,请说明理由。
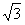 ),离心率为
),离心率为 。
。(1)求椭圆P的方程;
(2)是否存在过点E(0,-4)的直线l交椭圆P于点R,T,且满足
 ,若存在,求直线l的方程;若不存在,请说明理由。
,若存在,求直线l的方程;若不存在,请说明理由。 解:(1)设椭圆P的方程为 ,
,
由题意,得b=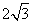 ,
, ,
,
∴ ,即
,即 ,
,
∴椭圆P的方程为 。
。
(2)假设存在满足题意的直线L,易知当直线的斜率不存在时,不满足题意;
故设直线L的斜率为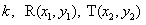 ,
,
 ,
,
∴ ,
,
由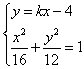 得
得 ,
,
由△>0,得 ,解得:
,解得: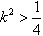 , ①
, ①
∴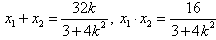 ,
,
∴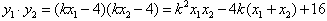 ,
,
故 ,
,
解得:k2=1, ②
由①、②解得k=±1,
∴直线l的方程为y=±x-4,
故存在直线l:x+y+4=0或x-y-4=0满足题意。
 ,
,由题意,得b=
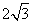 ,
, ,
,∴
 ,即
,即 ,
,∴椭圆P的方程为
 。
。(2)假设存在满足题意的直线L,易知当直线的斜率不存在时,不满足题意;
故设直线L的斜率为
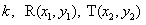 ,
, ,
,∴
 ,
,由
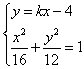 得
得 ,
,由△>0,得
 ,解得:
,解得: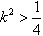 , ①
, ①∴
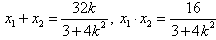 ,
,∴
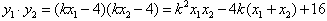 ,
,故
 ,
,解得:k2=1, ②
由①、②解得k=±1,
∴直线l的方程为y=±x-4,
故存在直线l:x+y+4=0或x-y-4=0满足题意。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目