题目内容
已知椭圆P的中心O在坐标原点,焦点在x轴上,且经过点A(0,2| 3 |
| 1 |
| 2 |
(1)求椭圆P的方程;
(2)是否存在过点E(0,-4)的直线l交椭圆P于点R,T,且满足
| OR |
| OT |
| 16 |
| 7 |
分析:(1)设椭圆P的方程为
+
═1 (a>b>0),由椭圆经过点A(0,2
),离心率为
,求得a和b的值,
从而求得椭圆P的方程.
(2)由
可得 x1+x2 和x1•x2 的值,可得y1•y2的值,根据
•
=
,求出k=±1,
从而得到直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
从而求得椭圆P的方程.
(2)由
|
| OR |
| OT |
| 16 |
| 7 |
从而得到直线l的方程.
解答:解:(1)设椭圆P的方程为
+
=1 (a>b>0),由题意得b=2
,
=
,
∴a=2c,b2=a2-c2=3c2,∴c=2,a=4,∴椭圆P的方程为:
+
= 1.
(2)假设存在满足题意的直线L.易知当直线的斜率不存在时,
•
<0,不满足题意.
故设直线L的斜率为k,R(x1,y1),T(x2,y2 ).∵
•
=
,∴x1•x2+y1•y2=
,
由
可得 (3+4k2 )x2-32kx+16=0,由△=(-32k)2-4(3+4k2)•16>0,
解得 k2>
①.
∴x1+x2=
,x1•x2=
,
∴y1•y2=(kx1-4 )(kx2-4)=k2 x1•x2-4k(x1+x2)+16,
∴x1•x2+y1•y2=
+
-
+16=
,∴k2=1 ②,
由①、②解得 k=±1,∴直线l的方程为 y=±x-4,
故存在直线l:x+y+4=0,或 x-y-4=0,满足题意.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| c |
| a |
| 1 |
| 2 |
∴a=2c,b2=a2-c2=3c2,∴c=2,a=4,∴椭圆P的方程为:
| x2 |
| 16 |
| y2 |
| 12 |
(2)假设存在满足题意的直线L.易知当直线的斜率不存在时,
| OR |
| OT |
故设直线L的斜率为k,R(x1,y1),T(x2,y2 ).∵
| OR |
| OT |
| 16 |
| 7 |
| 16 |
| 7 |
由
|
解得 k2>
| 1 |
| 4 |
∴x1+x2=
| 32k |
| 3+ 4k2 |
| 16 |
| 3+ 4k2 |
∴y1•y2=(kx1-4 )(kx2-4)=k2 x1•x2-4k(x1+x2)+16,
∴x1•x2+y1•y2=
| 16 |
| 3+ 4k2 |
| 16k2 |
| 3+ 4k2 |
| 128k2 |
| 3+ 4k2 |
| 16 |
| 7 |
由①、②解得 k=±1,∴直线l的方程为 y=±x-4,
故存在直线l:x+y+4=0,或 x-y-4=0,满足题意.
点评:本题考查求椭圆的标准方程的方法,直线和圆锥曲线的位置关系,两个向量的数量积公式,求出x1•x2和y1•y2 的值,是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
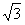 ),离心率为
),离心率为 。
。 ,若存在,求直线l的方程;若不存在,请说明理由。
,若存在,求直线l的方程;若不存在,请说明理由。