Question

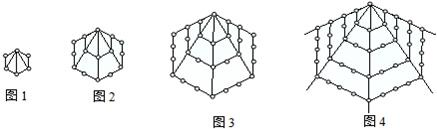
某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.

（1）求甲一次游戏中能中奖的概率;

（2）设这个正六边形的面积是6,求一次游戏中随机变量S的分布列及期望值.

 

Answer 1

【答案】

（1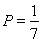）；（2）S的可能值为:0,1,2,3,其分布列为

S	0	1	2	3
P

．

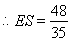【解析】

试题分析：（1）由题意可知，这是随机变量的等可能事件的概率问题，弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上共有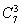种方法，当S最大时它的方法数有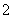种，当S最小时，即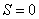共有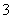种方法，一次游戏中能中奖的方法数有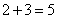种，由古典概率求法可得甲一次游戏中能中奖的概率；（2）设这个正六边形的面积是6,一次游戏中随机变量S的可能值为:0,1,2,3,分别求出它们的概率，得分布列，进而可求得期望值．

试题解析：（1）甲中奖的概率为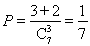

（2）S的可能值为:0,1,2,3,其分布列为

S	0	1	2	3
P

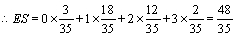
考点：古典概率，分布列及期望值．