题目内容
设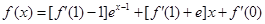
求 及
及 的单调区间
的单调区间
设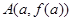 ,
,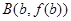
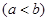 两点连线的斜率为
两点连线的斜率为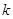 ,问是否存在常数
,问是否存在常数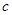 ,且
,且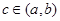 ,当
,当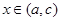 时有
时有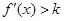 ,当
,当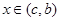 时有
时有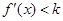 ;若存在,求出
;若存在,求出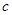 ,并证明之,若不存在说明理由.
,并证明之,若不存在说明理由.
【答案】
(1)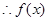 在
在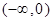 上单调递增,
上单调递增,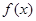 在
在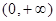 上单调递减
上单调递减
(2)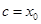 =
=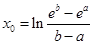 为所求.
为所求.
【解析】
试题分析:解;(1)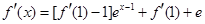
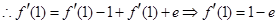

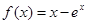
 ,当
,当 时
时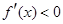
当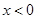 时
时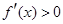
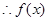 在
在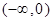 上单调递增,
上单调递增,
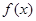 在
在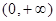 上单调递减.
5分
上单调递减.
5分
(2)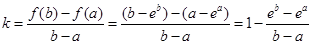
设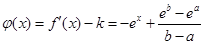
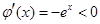
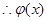 在
在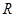 上单调递减
上单调递减
令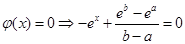
解得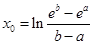
则当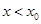 时,
时,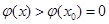
即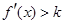
当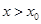 时,
时,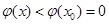
即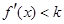 8分
8分
现在证明: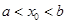
考察:
设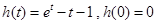
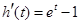 ,当
,当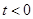 时,
时,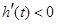 ,
,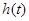 递减
递减
所以,当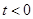 时,
时,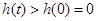 ,
,
即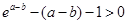
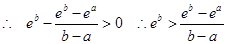
即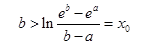 12分
12分
再考察: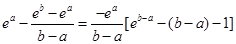
设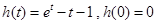
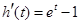 ,当
,当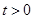 时,
时,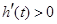 ,
,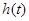 递增
递增
所以,当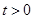 时,
时,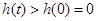 ,
,
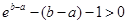
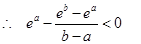
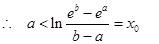
得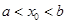 ,取
,取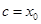 为所求.
14分
为所求.
14分
考点:导数的运用
点评:主要是考查了函数单调性,以及函数最值的运用和不等式的证明,属于难度题。

练习册系列答案
相关题目
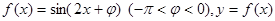 图像的一条对称轴是直线
图像的一条对称轴是直线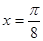
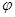 ;
;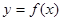 的单调区间及最值;
的单调区间及最值;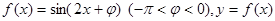 图像的一条对称轴是直线
图像的一条对称轴是直线
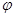 ;
;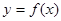 的单调区间及最值;
的单调区间及最值;