Question

设椭圆方程为x²+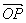=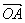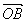1,过点M（0,1）的直线l交椭圆于点A、B，O是坐标原点，点P满足=（+），点N的坐标为（，）.当l绕点M旋转时，求：

（1）动点P的轨迹方程；

（2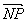）||的最小值与最大值.

Answer 1

思路解析：（1）设出l的斜率k，根据题设条件列出方程组，解得P点的坐标（用k表示），消去参数k即得.（2）则可化为区间上二次函数的最值问题.

（1）解法一：直线l过点M（0,1），设其斜率为k，则l的方程为y=kx+1.

设A(x₁,y₁)、B（x₂,y₂）,由题设可得点A、B的坐标（x₁,y₁）、（x₂,y₂）是方程组

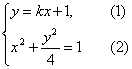
的解.

将（1）代入（2）并化简,得（4+k²）x²+2kx-3=0,

所以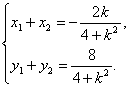

于是=（+）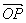

=(,)=(,).

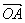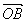设点P的坐标为（x,y），则

消去参数k,得4x²+y²-y=0.                                                       （3）

当k不存在时，A、B中点为坐标原点（0，0），也满足方程（3），所以点P的轨迹方程为4x²+y²-y=0.

解法二：设点P的坐标为（x,y），因A（x₁,y₁）、B(x₂,y₂)在椭圆上，

所以x₁²+=1,④,x₂²+=1.                                           ⑤

④-⑤,得x₁²-x₂²+(y₁²-y₂²)=0,

所以（x₁-x₂）(x₁+x₂)+(y₁-y₂)(y₁+y₂)=0.

当x₁≠x₂时，有x₁+x₂+(y₁+y₂)·=0,                      ⑥

并且                                                         ⑦

将⑦代入⑥并整理,得4x²+y²-y=0.                                              ⑧

当x₁=x₂时，点A、B的坐标为（0，2）、（0，-2），这时点P的坐标为（0，0）,也满足⑧,所以点P的轨迹方程为+=1.

(2)解：由点P的轨迹方程知x²≤，即-≤x≤.

所以|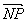|²=(x-)²+(y-)²=(x-)²+-4x²

=-3(x+)²+,

故当x=时，||取得最小值，最小值为；

当x=-时，||取得最大值，最大值为.