题目内容
设函数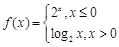 ,若对任意给定的
,若对任意给定的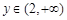 ,都存在唯一的
,都存在唯一的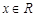 ,满足
,满足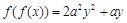 ,则正实数
,则正实数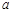 的最小值是( )
的最小值是( )
A.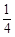 | B.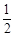 | C.2 | D.4 |
A
解析试题分析:当 ≤0时,
≤0时, =
=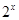 ,值域为(0,1],∴
,值域为(0,1],∴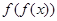 =
=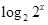 =
= ;当
;当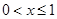 时,
时, =
=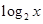 ,值域为(-
,值域为(-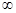 ,0],∴
,0],∴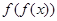 =
=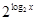 =
= ;当
;当 >1时,
>1时, =
=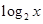 ,值域为(1,+
,值域为(1,+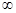 ),则
),则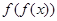 =
=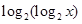 ,故
,故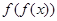 =
=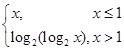 ,当
,当 ≤1时,
≤1时,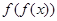 值域为(-
值域为(-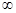 ,1],当
,1],当 >1时,
>1时,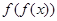 值域为(-
值域为(-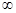 ,+
,+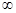 ),∵
),∵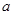 >0,∴
>0,∴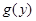 =
=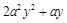 =
=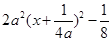 ,对称轴为
,对称轴为 ,故
,故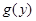 在(2,+
在(2,+ )上是增函数,则
)上是增函数,则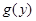 在
在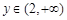 上的值域为(
上的值域为(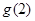 ,+
,+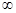 ),即(
),即(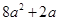 ,+
,+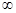 ),有题意知,
),有题意知,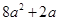 ≥1,解得
≥1,解得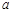 ≥
≥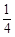 ,故正实数
,故正实数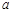 的最小值为
的最小值为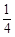 ,故选A.
,故选A.
考点:1.指数函数的图像性质;2.对数函数图像性质;3.二次函数图像性质;4.复合函数的值域;5.分类整合与转化化归思想.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
设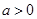 且
且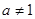 .若
.若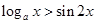 对
对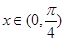 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )
A.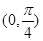 | B.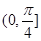 | C.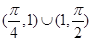 | D.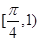 |
定义某种运算 ,运算原理如图所示,则式子
,运算原理如图所示,则式子 的值为( )
的值为( )
| A.-3 | B.-4 | C.-8 | D.0 |
三个数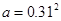 ,
, ,
,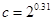 之间的大小关系( )
之间的大小关系( )
A.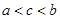 | B. | C. | D.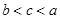 |
 的零点所在区间为( )
的零点所在区间为( )
| A.(0,1) | B.(-1,0) | C.(1,2) | D.(-2,-l) |
函数 的零点所在区间是( )
的零点所在区间是( )
A. | B. | C. | D. |
2log510+log50.25=( )
| A.0 | B.1 | C.2 | D.4 |
设α∈{-1,1, ,3},则使函数y=xα的定义域为R且为奇函数的所有α值为( )
,3},则使函数y=xα的定义域为R且为奇函数的所有α值为( )
| A.1,3 | B.-1,1 |
| C.-1,3 | D.-1,1,3 |
 ,
, ,沿对角线AC折成如图所示的四面体,二面角B-AC-D为
,沿对角线AC折成如图所示的四面体,二面角B-AC-D为 ,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )
,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )
