题目内容
函数 的零点所在区间是( )
的零点所在区间是( )
A. | B. | C. | D. |
C
解析试题分析:解: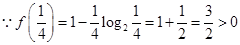

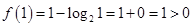

根据函数的零点存在性定理可以判断,函数 在区间
在区间 内存在零点.
内存在零点.
考点:1、对数的运算性质;2、函数的零点存在性定理.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
设函数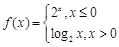 ,若对任意给定的
,若对任意给定的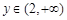 ,都存在唯一的
,都存在唯一的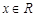 ,满足
,满足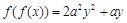 ,则正实数
,则正实数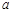 的最小值是( )
的最小值是( )
A.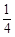 | B.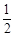 | C.2 | D.4 |
若函数 ,则
,则 (其中
(其中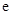 为自然对数的底数) ( )
为自然对数的底数) ( )
A. | B.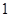 | C. | D. |
关于x的方程ex-1-|kx|=0(其中e=2.71828…是自然对数的底数)的有三个不同实根,则k的取值范围是
| A.{-2,0,2} | B.(1,+∞) | C.{k|k>e} | D.{k|k2>1} |
若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. | B. |
C. | D. |
已知函数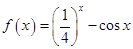 ,则
,则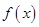 在
在 上的零点个数( )
上的零点个数( )
| A.1 | B.2 | C.3 | D.4 |
若 满足
满足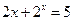 ,
,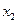 满足
满足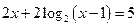 ,则
,则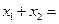 ( )
( )
A.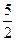 |
| B.3 |
C. |
| D.4 |
已知减函数f(x)的定义域是R,m,n∈R,如果不等式f(m)-f(n)>f(-m)-f(-n)成立,那么在下列给出的四个不等式中,正确的是( )
| A.m+n<0 | B.m+n>0 |
| C.m-n<0 | D.m-n>0 |
已知函数f(x)= 若f(2-x2)>f(x),则实数x的取值范围是( )
若f(2-x2)>f(x),则实数x的取值范围是( )
| A.(-∞,-1)∪(2,+∞) |
| B.(-∞,-2)∪(1,+∞) |
| C.(-1,2) |
| D.(-2,1) |