题目内容
设椭圆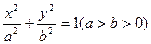 的焦点分别为
的焦点分别为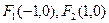 ,直线
,直线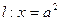 交
交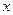 轴于点
轴于点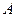 ,且
,且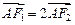 .
.
(1)试求椭圆的方程;
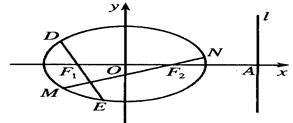
(2)过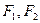 分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形
分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形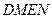 面积的最大值和最小值.
面积的最大值和最小值.
(1)由题意,

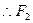 为
为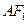 的中点
的中点 
即:椭圆方程为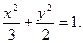 …………………(4分)
…………………(4分)
(2)当直线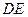 与
与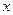 轴垂直时,
轴垂直时,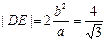 ,
,
此时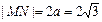 ,四边形
,四边形 的面积
的面积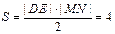 .
.
同理当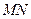 与
与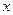 轴垂直时,也有四边形
轴垂直时,也有四边形 的面积
的面积 .
.
当直线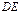 ,
, 均与
均与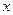 轴不垂直时,设
轴不垂直时,设 :
: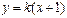 ,代入消去
,代入消去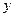 得:
得: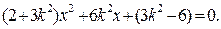
设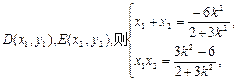
所以,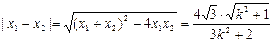 ,
,
所以, ,
, 
所以四边形的面积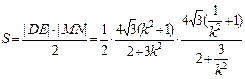
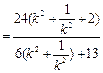
令
因为
 当
当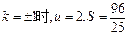 ,且S是以u为自变量的增函数,
,且S是以u为自变量的增函数,
所以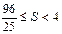 .
.
综上可知,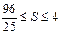 .故四
.故四 边形
边形 面积的最大值为4,最小值为
面积的最大值为4,最小值为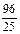 .
.
解析

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
将参数方程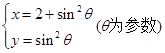 化为普通方程为( )
化为普通方程为( )
A.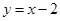 | B.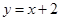 | C.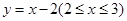 | D.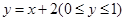 |
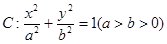 的离心率为
的离心率为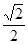 ,并且直线
,并且直线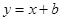 是抛物线
是抛物线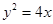 的一条切线。
的一条切线。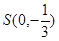 的动直线
的动直线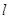 交椭圆
交椭圆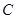 于
于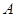 、
、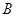 两点,试问:在直角坐标平面上是否存在一个定点
两点,试问:在直角坐标平面上是否存在一个定点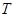 ,使得以
,使得以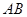 为直径的圆恒过点
为直径的圆恒过点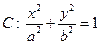 (
(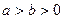 )的一个焦点坐标为
)的一个焦点坐标为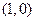 ,且长轴长是短轴长的
,且长轴长是短轴长的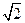 倍.
倍. 的方程;
的方程; 为坐标原点,椭圆
为坐标原点,椭圆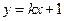 相交于两个不同的点
相交于两个不同的点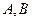 ,线段
,线段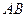 的中点为
的中点为 ,若直线
,若直线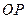 的斜率为
的斜率为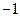 ,求△
,求△ 的面积.
的面积.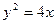 ,过点
,过点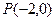 的直线AB交抛物线于点
的直线AB交抛物线于点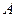 、
、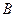 ,若线段
,若线段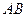 的垂直平分线交
的垂直平分线交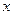 轴于点
轴于点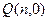 ,求
,求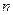 的取值范围.
的取值范围.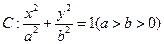 的离心率
的离心率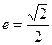 ,过右焦点
,过右焦点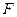
 的直线
的直线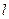 与椭圆
与椭圆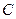 相交
相交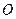 到直线
到直线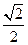
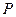 ,使得当直线
,使得当直线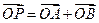 成
成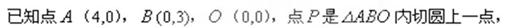
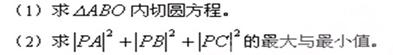
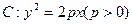 的准线为
的准线为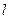 ,焦点为
,焦点为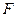 ,圆
,圆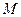 的圆心在
的圆心在 轴的正半轴上,且与
轴的正半轴上,且与 轴相切,过原点
轴相切,过原点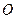 作倾斜角为
作倾斜角为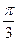 的直线
的直线 ,交
,交 于点
于点 ,交圆
,交圆 ,且
,且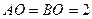
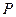 为抛物线C上的动点,求
为抛物线C上的动点,求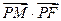 的最小值;
的最小值; 恒过一个定点,并求该定点的坐标.
恒过一个定点,并求该定点的坐标.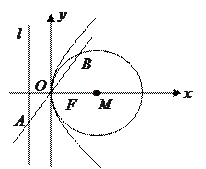
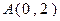 ,右焦点
,右焦点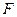 与点
与点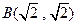 的距离为
的距离为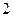 .
.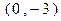 的直线
的直线 ,使直线
,使直线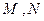 满足
满足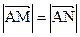 ?若存在,求出直线
?若存在,求出直线