题目内容
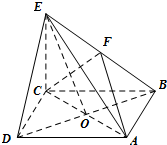 (2013•昌平区一模)在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
(2013•昌平区一模)在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.(Ⅰ)求证:DE∥平面ACF;
(Ⅱ)求证:BD⊥AE;
(Ⅲ)若AB=
| 2 |
| EG |
| EO |
分析:(Ⅰ)利用线面平行的判定定理证明DE∥平面ACF;
(Ⅱ)利用线面垂直的判定定理先证明BD⊥平面ACE,然后利用线面垂直的性质证明BD⊥AE;
(Ⅲ)利用线面垂直的性质,先假设CG⊥平面BDE,然后利用线面垂直的性质,确定G的位置即可.
(Ⅱ)利用线面垂直的判定定理先证明BD⊥平面ACE,然后利用线面垂直的性质证明BD⊥AE;
(Ⅲ)利用线面垂直的性质,先假设CG⊥平面BDE,然后利用线面垂直的性质,确定G的位置即可.
解答:解:(I)连接OF.由ABCD是正方形可知,点O为BD中点.
又F为BE的中点,
所以OF∥DE.
又OF?面ACF,DE?面ACF,
所以DE∥平面ACF….(4分)
(II) 证明:由EC⊥底面ABCD,BD?底面ABCD,
∴EC⊥BD,
由ABCD是正方形可知,AC⊥BD,
又AC∩EC=C,AC、E?平面ACE,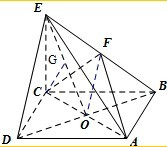
∴BD⊥平面ACE,
又AE?平面ACE,
∴BD⊥AE…(9分)
(III):在线段EO上存在点G,使CG⊥平面BDE.理由如下:
取EO中点G,连接CG,
在四棱锥E-ABCD中,AB=
CE,CO=
AB=CE,
∴CG⊥EO.
由(Ⅱ)可知,BD⊥平面ACE,而BD?平面BDE,
∴平面ACE⊥平面BDE,且平面ACE∩平面BDE=EO,
∵CG⊥EO,CG?平面ACE,
∴CG⊥平面BDE
故在线段EO上存在点G,使CG⊥平面BDE.
由G为EO中点,得
=
.…(14分)
又F为BE的中点,
所以OF∥DE.
又OF?面ACF,DE?面ACF,
所以DE∥平面ACF….(4分)
(II) 证明:由EC⊥底面ABCD,BD?底面ABCD,
∴EC⊥BD,
由ABCD是正方形可知,AC⊥BD,
又AC∩EC=C,AC、E?平面ACE,

∴BD⊥平面ACE,
又AE?平面ACE,
∴BD⊥AE…(9分)
(III):在线段EO上存在点G,使CG⊥平面BDE.理由如下:
取EO中点G,连接CG,
在四棱锥E-ABCD中,AB=
| 2 |
| ||
| 2 |
∴CG⊥EO.
由(Ⅱ)可知,BD⊥平面ACE,而BD?平面BDE,
∴平面ACE⊥平面BDE,且平面ACE∩平面BDE=EO,
∵CG⊥EO,CG?平面ACE,
∴CG⊥平面BDE
故在线段EO上存在点G,使CG⊥平面BDE.
由G为EO中点,得
| EG |
| EO |
| 1 |
| 2 |
点评:本题主要考查了空间直线和平面垂直的判定定理和性质定理的应用,要求熟练掌握相应的定理,综合性较强,难度较大.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 (2013•昌平区一模)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
(2013•昌平区一模)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: