题目内容
设函数f(x)=
，若f（t）＞2，则实数t的取值范围是（ ）
|
| A、（-∞，-1）∪（4，+∞） |
| B、（-∞，-3）∪（2，+∞） |
| C、（-∞，-4）∪（1，+∞） |
| D、（-∞，-2）∪（3，+∞） |
分析：本题利用图象解决．先画出函数f（x）的图象，和直线y=2，如图．观察图象可得不等式：f（t）＞2的解的集合．从而得出实数t的取值范围．
解答：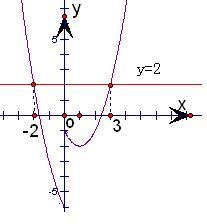
解：先画出函数f（x）的图象，和直线y=2，如图．
观察图象可得：
f（t）＞2，
则实数t的取值范围是：
（-∞，-2）∪（3，+∞）
故选D．
解：先画出函数f（x）的图象，和直线y=2，如图．观察图象可得：
f（t）＞2，
则实数t的取值范围是：
（-∞，-2）∪（3，+∞）
故选D．
点评：本题主要考查了一元二次不等式的解法，对于分段函数的有关不等式的解法，可依据图象法解决．
练习册系列答案
相关题目
设函数
设函数