题目内容
16.在锐角△ABC中,已知内角A、B、C所对的边分别为a,b,c,向量$\overrightarrow{m}$=(2sin(A+C),$\sqrt{3}$),$\overrightarrow{n}$=(cos2B,2cos$\frac{B}{2}$-1),且向量$\overrightarrow{m}$∥$\overrightarrow{n}$.(1)求角B的大小;
(2)如果b=1,求△ABC的面积S△ABC的最大值.
分析 (1)由条件利用两个向量共线的性质求得tan2B的值,再根据△ABC为锐角三角形,B的值.
(2)若b=1,则由余弦定理、基本不等式求得 ac 的最大值,可得△ABC面积为$\frac{1}{2}$ac•sinB,求得它的最大值.
解答 解:(1)∵向量$\overrightarrow{m}$=(2sin(A+C),$\sqrt{3}$),$\overrightarrow{n}$=(cos2B,2cos$\frac{B}{2}$-1),且向量$\overrightarrow{m}$∥$\overrightarrow{n}$.
∴2sin(A+C)(2cos2$\frac{B}{2}$-1)-$\sqrt{3}$cos2B=0,即 2sinBcosB=$\sqrt{3}$cos2B,
∴tan2B=$\frac{sin2B}{cos2B}$=$\sqrt{3}$.
再根据△ABC为锐角三角形,可得0<B<$\frac{π}{2}$,∴2B=$\frac{π}{3}$,B=$\frac{π}{6}$.
(2)若b=1,则由余弦定理可得 b2=1=a2+c2-2ac•cosB≥2ac-$\sqrt{3}$ac,
解得 ac≤$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,当且仅当a=c时,取等号,
故△ABC面积的最大值为$\frac{1}{2}$ac•sinB=$\frac{1}{2}$(2+$\sqrt{3}$)•$\frac{1}{2}$=$\frac{2+\sqrt{3}}{4}$.
点评 本题主要考查两个向量共线的性质,正弦定理和余弦定理、基本不等式的应用,考查了转化思想和计算能力,属于中档题.

练习册系列答案
相关题目
4.设点M(0,-5),N(0,5),△MNP的周长为36,则△MNP的顶点P的轨迹方程为( )
| A. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{25}$=1(x≠0) | B. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{144}$=1(x≠0) | ||
| C. | $\frac{{x}^{2}}{169}$+$\frac{{y}^{2}}{25}$=1(y≠0) | D. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{25}$=1(y≠0) |
1.已知函数f(x)=|log2|x-2||+k有四个零点x1,x2,x3,x4,则x1+x2+x3+x4+k的取值范围为( )
| A. | (8,+∞) | B. | (4,+∞) | C. | (-∞,8) | D. | (-∞,4) |
8.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,且|F1F2|=2c,若椭圆上存在点M使得$\frac{a}{sin∠M{F}_{1}{F}_{2}}$=$\frac{c}{sin∠M{F}_{2}{F}_{1}}$,则该椭圆离心率的取值范围为( )
| A. | (0,$\sqrt{2}$-1) | B. | ($\frac{\sqrt{2}}{2}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | ($\sqrt{2}$-1,1) |
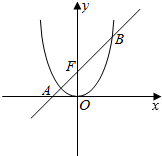 如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.
如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.