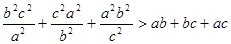题目内容
(本题12分)已知全集 ,集合A
,集合A R
R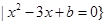 ,
,
B={x∈R|(x-2)(x2+3x-4)=0}
(1)若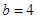 时,存在集合M使得A
时,存在集合M使得A M
M B,求出所有这样的集合M;
B,求出所有这样的集合M;
(2)集合A、B是否能满足∁UB A=
A= ?若能,求实数
?若能,求实数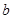 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
(1)用列举法可得这样的M共有如下6个:{-4}、{1}、{2}、{-4,1}、{-4,2}、{1,2}。
(2)当且仅当P=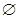 或P={1,2}时,
或P={1,2}时,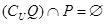 ,
,
实数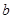 的取值范围是
的取值范围是 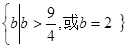
【解析】解:(1)易知P=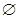 ,且
,且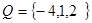 ,由已知M应该是一个非空集合,
,由已知M应该是一个非空集合,
且是Q的一个真子集,∴用列举法可得这样的M共有如下6个:
{-4}、{1}、{2}、{-4,1}、{-4,2}、{1,2}。 ……………………………….4分
(2)由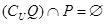 得
得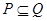 , ………………………………………………….6分
, ………………………………………………….6分
当P=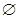 时,P是Q的一个子集,此时
时,P是Q的一个子集,此时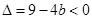 ,∴
,∴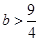 ; ……………8分
; ……………8分
若P≠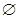 ,∴
,∴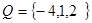 ,
,
当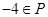 时,则得到P=
时,则得到P=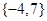 不可能为Q的一个子集,
不可能为Q的一个子集,
当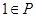 时,
时,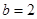 ,此时P={1,2}是Q的子集,
,此时P={1,2}是Q的子集,
当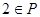 时,
时,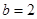 ,此时P={1,2}是Q的子集;
………………………………10分
,此时P={1,2}是Q的子集;
………………………………10分
综上可知:当且仅当P=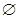 或P={1,2}时,
或P={1,2}时,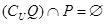 ,
,
∴实数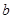 的取值范围是
的取值范围是 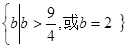 ……………………………12分
……………………………12分

(本题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中,![]() 还喜欢打羽毛球,
还喜欢打羽毛球,![]() 还喜欢打乒乓球,
还喜欢打乒乓球,![]() 还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)![]()
(本题满分12分)为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 。
。
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中, 还喜欢打羽毛球,
还喜欢打羽毛球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求 和
和 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
|
|
0.15[ |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7. 879 |
10.828 |
(参考公式: ,其中
,其中 )
)

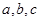 为都大于1的不全相等的正实数,
为都大于1的不全相等的正实数,