题目内容
1．已知O为四边形ABCD所在平面内的一点，且向量$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}，\overrightarrow{OD}$满足等式$\overrightarrow{OA}$+$\overrightarrow{OC}$=$\overrightarrow{OB}$+$\overrightarrow{OD}$．（1）作图并观察四边形ABCD的形状；
（2）四边形ABCD有什么特性？试证明你的猜想．
分析 （1）直接作图即可；
（2）结论：四边形ABCD为平行四边形；将表达式$\overrightarrow{OA}$+$\overrightarrow{OC}$=$\overrightarrow{OB}$+$\overrightarrow{OD}$变形，利用向量减法运算法则即得结果．
解答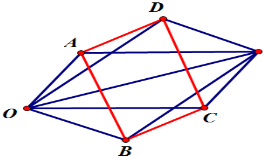 
解：（1）如右图；
（2）猜想：四边形ABCD为平行四边形；
证明如下：
∵$\overrightarrow{OA}$+$\overrightarrow{OC}$=$\overrightarrow{OB}$+$\overrightarrow{OD}$
∴$\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{OD}-\overrightarrow{OA}$，
即$\overrightarrow{BC}=\overrightarrow{AD}$，
故四边形ABCD为平行四边形．
点评 本题考查向量减法的运算法则，对表达式的灵活变形是解题的关键，属于基础题．
练习册系列答案
相关题目
11．已知{an}（n∈N+）是各项为正数的等比数列，q是其公比，Tn是前n项的积，且T5＜T6，T6=T7＞T8，则下列判断正确的是（ ）
| A． | q＞1 | B． | 0＜a1＜1 | C． | 0＜a6a8＜1 | D． | T9＜T5 |
9．在△ABC中，a=7，c=5，则sinA：sinC的值是（ ）
| A． | $\frac{7}{5}$ | B． | $\frac{5}{7}$ | C． | $\frac{7}{12}$ | D． | $\frac{5}{12}$ |
6．在△ABC中，∠A、∠B、∠C的对边分别为a，b，c，若∠A=60°，b=1，c=4，则$\frac{a+b+c}{sinA+sinB+sinC}$的值为（ ）
| A． | $\frac{2\sqrt{39}}{3}$ | B． | $\frac{26\sqrt{3}}{3}$ | C． | $\frac{8\sqrt{3}}{3}$ | D． | 2$\sqrt{3}$ |
