题目内容
15.已知 f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}+5x}{6},0≤x≤3}\\{10-2x,3<x≤5}\end{array}\right.$,若存在实数m,n∈[0,5],且m<n使得f(x)在区间[m,n]上的值域为[m,n],则这样的实数对(m,n)共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
分析 作函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}+5x}{6},0≤x≤3}\\{10-2x,3<x≤5}\end{array}\right.$的图象,分类讨论以确定函数的定义域与值域,从而解得.
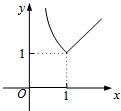
解答  解:作函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}+5x}{6},0≤x≤3}\\{10-2x,3<x≤5}\end{array}\right.$的图象如右图,
解:作函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}+5x}{6},0≤x≤3}\\{10-2x,3<x≤5}\end{array}\right.$的图象如右图,
①当0≤m<n≤3时,f(x)=$\frac{{x}^{2}+5x}{6}$在区间[m,n]单调递增,
则$\left\{\begin{array}{l}{f(m)=m}\\{f(n)=n}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{{m}^{2}+5m}{6}=m}\\{\frac{{n}^{2}+5n}{6}=n}\end{array}\right.$;
解得,m=0,n=1;
②当3≤m<n≤5时,f(x)=10-2x在[m,n]单调递减,则
$\left\{\begin{array}{l}{f(m)=n}\\{f(n)=m}\end{array}\right.$,即$\left\{\begin{array}{l}{10-2m=n}\\{10-2n=m}\end{array}\right.$,
解得,m=n=$\frac{10}{3}$(舍);
③当0≤m<3<n<5时,可知函数的最大值为f(3)=4=n,
从而可得函数的定义域及值域为[m,4],而f(4)=2,
(i)当m=2时,定义域[2,4],f(2)=$\frac{7}{3}$>f(4)=2,故值域为[2,4]符合题意;
(ii)当m<2时,f(m)=$\frac{{m}^{2}+5m}{6}$=m可得m=1,n=4,或m=0,n=4;符合题意;
综上可得符合题意的有(0,1),(0,4),(1,4),(2,4);
故选:D.
点评 本题考查了数形结合的思想的应用及分类讨论的思想应用.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | -$\frac{1}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | 0 | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | -2或2 | B. | -9或3 | C. | -1或1 | D. | -3或1 |