题目内容
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为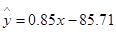 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
D.
解析试题分析:根据回归方程为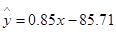 知,
知,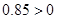 ,所以
,所以 与
与 具有正的线性相关关系,故
具有正的线性相关关系,故 正确;又因为回归直线过样本点的中心
正确;又因为回归直线过样本点的中心 ,故
,故 正确;因为
正确;因为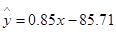 ,所以该大学某女生身高增加lcm,则其体重约增加0.85kg,故
,所以该大学某女生身高增加lcm,则其体重约增加0.85kg,故 正确;当
正确;当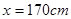 时,
时,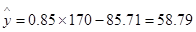 ,但这是预测值,不可断定其体重为58.79kg,故
,但这是预测值,不可断定其体重为58.79kg,故 不正确.
不正确.
考点:回归分析的初步应用.

练习册系列答案
相关题目
设有一个回归直线方程为 ,则变量x增加一个单位时
,则变量x增加一个单位时
| A.y平均增加1.5个单位 | B.y平均增加2个单位 |
| C.y平均减少1.5个单位 | D.y平均减少2个单位 |
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间 与数学成绩
与数学成绩 进行数据收集如下:
进行数据收集如下:
| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
 ,则点
,则点 与直线
与直线 的位置关系是( )
的位置关系是( )点在直线左侧 B.点在直线右侧 C.点在直线上 D.无法确定
两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1的相关指数 为0.98 为0.98 | B.模型2的相关指数 为0.80 为0.80 |
C.模型3的相关指数 为0.50 为0.50 | D.模型4的相关指数 为0.25 为0.25 |
有一个容量为200的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
| A.18 | B.36 | C.54 | D.72 |

 ,
,

 ,
,
 与
与 之间的一组抽样数据如下:
之间的一组抽样数据如下: 必过点( )
必过点( ) B.
B.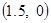 C.
C.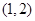 D.
D.

 ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )