题目内容
从原点O向圆x2+y2-12y+27=0作两条切线，则该圆夹在两条切线间的劣弧长为 ________．
2π
分析：把圆的方程化为标准方程后，找出圆心C的坐标和圆的半径r，根据AC与BC为圆的半径等于3，OC的长度等于6，利用直角三角形中一直角边等于斜边的一半得到角AOB等于2×30°，然后根据四边形的内角和定理求出角BCA的度数，然后由角BCA的度数和圆的半径，利用弧长公式即可求出该圆夹在两条切线间的劣弧长．
解答：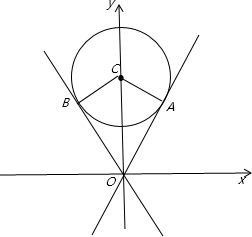
解：把圆的方程化为标准方程为：x2+（y-6）2=9，
得到圆心C的坐标为（0，6），圆的半径r=3，
由圆切线的性质可知，∠BOC=∠AOC=90°，且AC=BC=3，OC=3，
则∠AOB=∠BOC+∠AOC=60°，所以∠ACB=120°，
所以该圆夹在两条切线间的劣弧长l=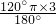
=2π．
故答案为：2π
点评：此题考查学生掌握直线与圆相切时所满足的条件，掌握直角三角形的性质，灵活运用弧长公式化简求值，是一道综合题．
分析：把圆的方程化为标准方程后，找出圆心C的坐标和圆的半径r，根据AC与BC为圆的半径等于3，OC的长度等于6，利用直角三角形中一直角边等于斜边的一半得到角AOB等于2×30°，然后根据四边形的内角和定理求出角BCA的度数，然后由角BCA的度数和圆的半径，利用弧长公式即可求出该圆夹在两条切线间的劣弧长．
解答：
解：把圆的方程化为标准方程为：x2+（y-6）2=9，得到圆心C的坐标为（0，6），圆的半径r=3，
由圆切线的性质可知，∠BOC=∠AOC=90°，且AC=BC=3，OC=3，
则∠AOB=∠BOC+∠AOC=60°，所以∠ACB=120°，
所以该圆夹在两条切线间的劣弧长l=
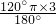=2π．故答案为：2π
点评：此题考查学生掌握直线与圆相切时所满足的条件，掌握直角三角形的性质，灵活运用弧长公式化简求值，是一道综合题．
练习册系列答案
口算能手系列答案
相关题目