题目内容
已知圆C:x2+y2+2x-4y+3=0;
(1)若圆C的切线在x轴,y轴上的截距相等,求此切线方程;
(2)求圆C关于直线x-y-3=0的对称的圆方程
(3)从圆C外一点P(x1,y1)向圆引一条切线,切点为M,O为原点,且有|PM|=|PO|,求使|PM|最小的P点的坐标.
(1)若圆C的切线在x轴,y轴上的截距相等,求此切线方程;
(2)求圆C关于直线x-y-3=0的对称的圆方程
(3)从圆C外一点P(x1,y1)向圆引一条切线,切点为M,O为原点,且有|PM|=|PO|,求使|PM|最小的P点的坐标.
分析:(1)求出圆心和半径,设直线方程为x+y-a=0或y=kx,由圆心C到切线的距离等于半径,求出待定系数a和k的值,即可得到所求切线方程;
(2)求出圆心关于直线x-y-3=0 的对称点坐标,而对称圆的半径和已知圆的半径相等,由圆方程的一般式即可求出对称圆的方程;
(3)由切线的性质得到△PCM为直角三角形,利用勾股定理得|PC|2=|PM|2+r2,由|PM|2=|PO|2利用两点间的距离公式化简可得点P的轨迹为2x1-4y1+3=0,再求得原点在直线2x-4y+3=0上的射影点,即得使|PM|最小的P点的坐标.
(2)求出圆心关于直线x-y-3=0 的对称点坐标,而对称圆的半径和已知圆的半径相等,由圆方程的一般式即可求出对称圆的方程;
(3)由切线的性质得到△PCM为直角三角形,利用勾股定理得|PC|2=|PM|2+r2,由|PM|2=|PO|2利用两点间的距离公式化简可得点P的轨迹为2x1-4y1+3=0,再求得原点在直线2x-4y+3=0上的射影点,即得使|PM|最小的P点的坐标.
解答:解:(1)圆C:x2+y2+2x-4y+3=0即(x+1)2+(y-2)2=2,
表示圆心为C(-1,2),半径等于
的圆.
设斜率为-1的切线方程为x+y-a=0,过原点的切线方程为kx-y=0,
则圆心C到切线的距离等于半径,
可得:
=
,求得a=-1或3.
再由
=
,求得k=2±
,
故所求的切线的方程为x+y-3=0或x+y+1=0或y=(2±
)x;
(2)由(1)圆C(x+1)2+(y-2)2=2的圆心在(-1,2),半径等于
.
∵点P(m,n)关于直线x-y-3=0的对称的点为P'(n+3,m-3)
∴点(-1,2)关于直线x-y-3=0对称的点的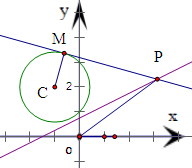
坐标为(2+3,-1-3)即(5,-4),
故圆C关于直线x-y-3=0的对称的圆方程是 (x-5)2+(y+4)2=2;
(3)设P的坐标为(x,y)
由于|PC|2=|PM|2+|CM|2=|PM|2+r2,
∴|PM|2=|PC|2-r2.
又∵|PM|=|PO|,∴|PC|2-r2=|PO|2,
∴(x1+1)2+(y1-2)2-2=x12+y12.
∴2x1-4y1+3=0即为动点P的轨迹方程.
∵原点在直线2x-4y+3=0上的射影点为(-
,
),
∴使|PM|最小的P点的坐标为(-
,
).
表示圆心为C(-1,2),半径等于
| 2 |
设斜率为-1的切线方程为x+y-a=0,过原点的切线方程为kx-y=0,
则圆心C到切线的距离等于半径,
可得:
| 2 |
| |-1+2-a| | ||
|
再由
| 2 |
| |-k+2| | ||
|
| 6 |
故所求的切线的方程为x+y-3=0或x+y+1=0或y=(2±
| 6 |
(2)由(1)圆C(x+1)2+(y-2)2=2的圆心在(-1,2),半径等于
| 2 |
∵点P(m,n)关于直线x-y-3=0的对称的点为P'(n+3,m-3)
∴点(-1,2)关于直线x-y-3=0对称的点的

坐标为(2+3,-1-3)即(5,-4),
故圆C关于直线x-y-3=0的对称的圆方程是 (x-5)2+(y+4)2=2;
(3)设P的坐标为(x,y)
由于|PC|2=|PM|2+|CM|2=|PM|2+r2,
∴|PM|2=|PC|2-r2.
又∵|PM|=|PO|,∴|PC|2-r2=|PO|2,
∴(x1+1)2+(y1-2)2-2=x12+y12.
∴2x1-4y1+3=0即为动点P的轨迹方程.
∵原点在直线2x-4y+3=0上的射影点为(-
| 3 |
| 10 |
| 3 |
| 5 |
∴使|PM|最小的P点的坐标为(-
| 3 |
| 10 |
| 3 |
| 5 |
点评:本题给出圆的方程,求圆在轴上截距相等的切线方程和圆关于直线对称的圆的方程.着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.