题目内容
已知函数f(x)=x3+ax2+b(a∈R,b∈R)(Ⅰ)若 a>0,且f(x)的极大值为5,极小值1,求f(x)的解析式;
(Ⅱ)若f(x)在(-∞,-
 )上是增函数,求a的取值范围.
)上是增函数,求a的取值范围.
【答案】分析:(Ⅰ)求导数,利用导数和极值之间的关系建立方程组,求f(x)的解析式;
(Ⅱ)利用f(x)在(-∞,- )上是增函数,则f'(x)≥0在(-∞,-
)上是增函数,则f'(x)≥0在(-∞,- )恒成立,然后分类讨论.
)恒成立,然后分类讨论.
解答:解:(I)∵f(x)=x3+ax2+b,所以f'(x)=3x2+2ax,由f'(x)=3x2+2ax=0,解得x=0或x=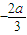 ,
,
因为 a>0,所以x=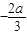 <0,
<0,
当f'(x)>0时,解得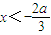 或x>0,此时函数单调递增.
或x>0,此时函数单调递增.
当f'(x)0时,解得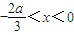 ,此时函数单调递减.
,此时函数单调递减.
所以当x=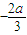 时,函数取得极大值,当x=0时,函数取得极小值.
时,函数取得极大值,当x=0时,函数取得极小值.
即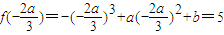 ,f(0)=b=1,
,f(0)=b=1,
解得a=3,b=1.
∴所求的函数解析式是f(x)=-x3+3x2+1.…(6分)
(II)由上问知当x=0或x=-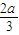 时,f'(x)=0.
时,f'(x)=0.
①当a>0时,x=-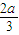 <0.函数f(x)在(-∞,-
<0.函数f(x)在(-∞,-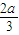 )和(0,+∞)上是单调递增函数,在(-
)和(0,+∞)上是单调递增函数,在(- ,0)上是单调递减函数.
,0)上是单调递减函数.
∴若f(x)在(-∞,- )上是增函数,则必有
)上是增函数,则必有 ,解得
,解得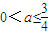 .
.
②当a<0时,- >0.函数f(x)在(-∞,0)和(-
>0.函数f(x)在(-∞,0)和(- ,+∞)上是单调递增函数,
,+∞)上是单调递增函数,
在(0,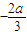 )上是单调递减函数.显然满足f(x)在(-∞,-
)上是单调递减函数.显然满足f(x)在(-∞,- )上是增函数.
)上是增函数.
③当a=0时,-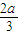 =0.函数f(x)在(-∞,+∞)上是单调递增函数,
=0.函数f(x)在(-∞,+∞)上是单调递增函数,
也满足f(x)在(-∞,- )上是增函数.
)上是增函数.
∴综合上述三种情况,所求a的取值范围为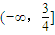 .…(12分)
.…(12分)
点评:本题主要考查函数的单调性,极值与导数之间的关系,要求熟练掌握导数在研究函数中的应用.
(Ⅱ)利用f(x)在(-∞,-
 )上是增函数,则f'(x)≥0在(-∞,-
)上是增函数,则f'(x)≥0在(-∞,- )恒成立,然后分类讨论.
)恒成立,然后分类讨论.解答:解:(I)∵f(x)=x3+ax2+b,所以f'(x)=3x2+2ax,由f'(x)=3x2+2ax=0,解得x=0或x=
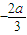 ,
,因为 a>0,所以x=
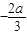 <0,
<0,当f'(x)>0时,解得
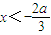 或x>0,此时函数单调递增.
或x>0,此时函数单调递增.当f'(x)0时,解得
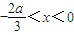 ,此时函数单调递减.
,此时函数单调递减.所以当x=
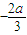 时,函数取得极大值,当x=0时,函数取得极小值.
时,函数取得极大值,当x=0时,函数取得极小值.即
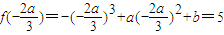 ,f(0)=b=1,
,f(0)=b=1,解得a=3,b=1.
∴所求的函数解析式是f(x)=-x3+3x2+1.…(6分)
(II)由上问知当x=0或x=-
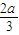 时,f'(x)=0.
时,f'(x)=0.①当a>0时,x=-
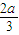 <0.函数f(x)在(-∞,-
<0.函数f(x)在(-∞,-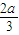 )和(0,+∞)上是单调递增函数,在(-
)和(0,+∞)上是单调递增函数,在(- ,0)上是单调递减函数.
,0)上是单调递减函数.∴若f(x)在(-∞,-
 )上是增函数,则必有
)上是增函数,则必有 ,解得
,解得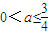 .
.②当a<0时,-
 >0.函数f(x)在(-∞,0)和(-
>0.函数f(x)在(-∞,0)和(- ,+∞)上是单调递增函数,
,+∞)上是单调递增函数,在(0,
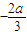 )上是单调递减函数.显然满足f(x)在(-∞,-
)上是单调递减函数.显然满足f(x)在(-∞,- )上是增函数.
)上是增函数.③当a=0时,-
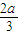 =0.函数f(x)在(-∞,+∞)上是单调递增函数,
=0.函数f(x)在(-∞,+∞)上是单调递增函数,也满足f(x)在(-∞,-
 )上是增函数.
)上是增函数.∴综合上述三种情况,所求a的取值范围为
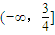 .…(12分)
.…(12分)点评:本题主要考查函数的单调性,极值与导数之间的关系,要求熟练掌握导数在研究函数中的应用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|