Question

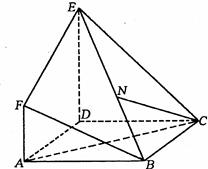如图，在多面体ABCDEF中，底面ABCD是正方形，AF⊥平面ABCD，DE∥AF，AB=DE=2
（1）求证：BE⊥AC；
（2）点N在棱BE上，当BN的长度为多少时，直线CN与平面ADE成30°角？

Answer 1

分析：（1）连接BD，ABCD是正方形，AC⊥BD．得出BD是斜线EB在平面ABCD内的射影，由三垂线定理得到BE⊥AC．
（2）以D为原点，DA、DC、DE为x，y，z建立空间直角坐标系，求出各个顶点的坐标，进而求出平面AED的法向量，代入向量夹角公式，即可得到直线CN与平面ADE所成角的大小；

解答：证明：（1）连接BD，
∵ABCD是正方形，
∴AC⊥BD．
又ED⊥底面ABCD，
∴BD是斜线EB在平面ABCD内的射影．
∴BE⊥AC．
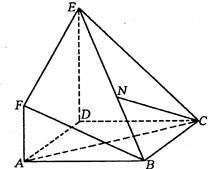（2）以D为原点，DA、DC、DE为x，y，z建立空间直角坐标系，
则A（2，0，0）、B（2，2，0），C（0，2，0），E（0，0，2）
设N（x，y，z），且

BN

=λ

BE

（0≤λ≤1）
则N（2-2λ，2-2λ，2λ），∴

CN

=(2-2λ，-2λ，2λ)
平面ADE的法向量为

n

=(0，1，0)
则cos＜

n

，

CN

＞=

2λ

(2-2λ)2+(2λ)2+(2λ)2

=

1

2

，
解得λ=

2

-1
又BE=2

3

，∴BN=λBE=(

2

-1)•2

3

=2

6

-2

3

即当BN=2

6

-2

3

时，直线CN与平面ADE成30°角

点评：本题考查的知识点是直线与平面垂直的性质及用空间向量求直线与平面的夹角及求法，在使用向量法求求直线与平面的夹角的大小时，建立坐标系，求出平面的法向量是关键．