题目内容
9.函数y=x+$\frac{4}{x}$在[2,4]上的最小值是4,最大值是5.分析 求出函数的导数,判断函数的单调性,即可得到函数的最值.
解答 解:函数y=x+$\frac{4}{x}$的导数为
y′=1-$\frac{4}{{x}^{2}}$,
由x∈[2,4]可得$\frac{4}{{x}^{2}}$∈[$\frac{1}{4}$,1],
即有y′>0,
则函数在[2,4]递增,
即有x=2时,ymin=2+2=4;
x=4时,ymax=4+1=5.
故答案为:4,5.
点评 本题考查函数的最值的求法,考查导数的运用,以及函数的单调性的运用,属于基础题.

练习册系列答案
相关题目
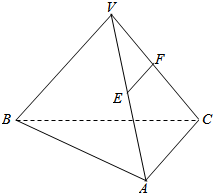 如图,在三棱锥V-ABC中,点E∈VA,点F∈VC,经过EF作一个截面γ,使VB∥平面γ,试作平面γ与三棱锥V-ABC表面的交线.
如图,在三棱锥V-ABC中,点E∈VA,点F∈VC,经过EF作一个截面γ,使VB∥平面γ,试作平面γ与三棱锥V-ABC表面的交线.