题目内容
19.已知二次函数f(x)=x2-2x+2.(1)当x∈[0,4]时,求f(x)的最大值、最小值;
(2)当x∈[t,t+1]时,t∈R,求f(x)的最大、最小值.
分析 (1)根据二次函数f(x)=x2-2x+2的图象和性质,分析当x∈[0,4]时,函数的单调性,进而可得f(x)的最大值、最小值;
(2)先将函数f(x)进行配方,得到对称轴,然后讨论对称轴与区间[t,t+1]的位置关系,从而得到最小值和最大值.、
解答 解:二次函数f(x)=x2-2x+2的图象是开口朝上,且以直线x=1为对称轴的抛物线,
(1)当x∈[0,4]时,
函数在[0,1]上为减函数,在[1,4]上为增函数,
故当x=1时,函数取最小值1,当x=4时,函数取最大值10,
(2)当t>1时,f(x)在[t,t+1]上是增函数,
∴当x=t时,函数取最小值t2-2t+2,
当x=t+1时,函数取最大值t2+1,
当$\frac{1}{2}$≤t≤1时,
当x=1时,函数取最小值1,
当x=t+1时,函数取最大值t2+1,
当0≤t$<\frac{1}{2}$时,
当x=1时,函数取最小值1,
当x=t时,函数取最大值t2-2t+2,
当t+1<1,即t<0时,f(x)在区间[t,t+1]上是减函数,
当x=t时,函数取最大值t2-2t+2,
当x=t+1时,函数取最小值t2+1,
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
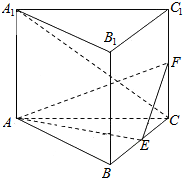 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.