题目内容
 [选做题]
[选做题]A.(选修4-1:几何证明选讲)
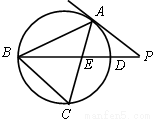
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
∠ABC=60°,PD=1,BD=8,求BC的长.
B.(选修4-2:矩阵与变换)
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(Ⅰ)求矩阵M的逆矩阵M-1;
(Ⅱ)设直线l在变换M作用下得到了直线m:2x-y=4,求l的方程.
C.(选修4-4:坐标系与参数方程)
在极坐标系中,设圆ρ=3上的点到直线ρ(cosθ+
| 3 |
D.(选修4-5:不等式选讲)
设a,b,c为正数且a+b+c=1,求证:(a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 100 |
| 3 |
分析:A.由切割线定理,得到PA2=PD•BD,从而有AE=PA=3,再用弦切角得到∠PAE=∠ABC=60°,可得△PAE是边长为3的等边三角形.然后在在△ADE中利用余弦定理,算出得AD=
,最后利用△AED∽△BEC,由对应边成比例得到BC=2AD=2
.
B.(I)设M=
,利用矩阵乘法的法则,结合题意列出关于a、b、c、d的方程组并解之,可得矩阵M,再用二阶矩阵逆矩阵的公式,可算出矩阵M的逆矩阵M-1;
(II)设l上的点(x,y)被M变换为m上的点(x',y'),根据矩阵变换的公式找到用x、y表示x'、y'的式子,再将此对应的点的坐标代入直线m方程,化简整理即得直线l的方程.
C.圆ρ=3化成普通方程:x2+y2=9,直线ρ(cosθ+
sinθ)=2的普通方程为x+
y-2=0.设圆上的点A(3cosα,3sinα),利用点到直线的距离公式结合正弦函数的最值,可算出圆上的点到直线距离的最大值.
D.将不等式左边变形后,利用柯西不等式,再将a+b+c=1代入,将所得不等式再整理,即得要证明的不等式恒成立.
| 7 |
| 7 |
B.(I)设M=
|
(II)设l上的点(x,y)被M变换为m上的点(x',y'),根据矩阵变换的公式找到用x、y表示x'、y'的式子,再将此对应的点的坐标代入直线m方程,化简整理即得直线l的方程.
C.圆ρ=3化成普通方程:x2+y2=9,直线ρ(cosθ+
| 3 |
| 3 |
D.将不等式左边变形后,利用柯西不等式,再将a+b+c=1代入,将所得不等式再整理,即得要证明的不等式恒成立.
解答:A.解:∵PA是⊙O的切线,∴PA2=PD•BD,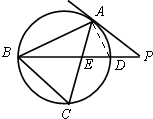
∵PB=PD+BD=1+8=9,∴PA2=1×9=9,可得PA=3,AE=PA=3,
∵PA是⊙O的切线,∴∠PAE=∠ABC=60°,可得△PAE是边长为3的等边三角形
连接AD,在△ADE中,AE=3,DE=2,得AD=
=
又∵圆中△AED∽△BEC,
∴
=
=
,可得BC=2AD=2
B.解:(Ⅰ)设M=
,则有
=
,
=
,
所以
,且
,解得
所以M=
,从而M-1=
(Ⅱ)因为
=
,所以
∵l在变换M作用下得到了直线m:2x'-y'=4,
∴代入得:2(x+2y)-(3x+4y)=4,化简得x+4=0,
∴直线l的方程方程为x+4=0
C.解:将极坐标方程ρ=3转化为普通方程:x2+y2=9
直线ρ(cosθ+
sinθ)=2可化为x+
y-2=0
在x2+y2=9上任取一点A(3cosα,3sinα),则
点A到直线的距离为d=
=
,
当sin(α+
)=-1时,d的最大值为4.
D.证明:左边=
(12+12+12)[(a+
)2+(b+
)2+(c+
)2]
≥
[1×(a+
)+1×(b+
)+1×(c+
)]2=
[1+(
+
+
)]2=
[1+(a+b+c)(
+
+
)]2
∵a+b+c=1,可得(a+b+c)(
+
+
) ≥(a•
+b•
+c•
)=9
∴原不等式的左边≥
(1+9)2=
,即不等式(a+
)2+(b+
)2+(c+
)2≥
成立.

∵PB=PD+BD=1+8=9,∴PA2=1×9=9,可得PA=3,AE=PA=3,
∵PA是⊙O的切线,∴∠PAE=∠ABC=60°,可得△PAE是边长为3的等边三角形
连接AD,在△ADE中,AE=3,DE=2,得AD=
| AE2+DE2-2•AE•DEcos60° |
| 7 |
又∵圆中△AED∽△BEC,
∴
| AD |
| BC |
| AE |
| BE |
| 1 |
| 2 |
| 7 |
B.解:(Ⅰ)设M=
|
|
|
|
|
|
|
所以
|
|
|
所以M=
|
|
(Ⅱ)因为
|
|
|
∵l在变换M作用下得到了直线m:2x'-y'=4,
∴代入得:2(x+2y)-(3x+4y)=4,化简得x+4=0,
∴直线l的方程方程为x+4=0
C.解:将极坐标方程ρ=3转化为普通方程:x2+y2=9
直线ρ(cosθ+
| 3 |
| 3 |
在x2+y2=9上任取一点A(3cosα,3sinα),则
点A到直线的距离为d=
|3cosα+3
| ||
| 2 |
|6sin(α+
| ||
| 2 |
当sin(α+
| π |
| 6 |
D.证明:左边=
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
≥
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
∵a+b+c=1,可得(a+b+c)(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
∴原不等式的左边≥
| 1 |
| 3 |
| 100 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 100 |
| 3 |
点评:本题以平面几何证明、矩阵及矩阵变换、参数方程与极坐标和不等式选讲为载体,考查了同学们对数学选修知识的理解与掌握情况,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•江苏二模)选做题
(2012•江苏二模)选做题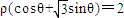 的距离为d,求d的最大值.
的距离为d,求d的最大值.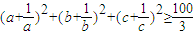 .
.