题目内容
已知函数
(I)当 时,求
时,求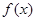 在[1,
在[1, ]上的取值范围。
]上的取值范围。
(II)若 在[1,
在[1, ]上为增函数,求a的取值范围。
]上为增函数,求a的取值范围。
【答案】
(1)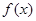 取值范围为[
取值范围为[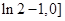 (2)
(2)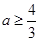
【解析】
试题分析:解:(1)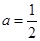 时
时 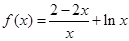
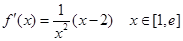
当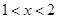 时
时 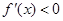
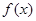 在[1,2)上
在[1,2)上
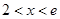 时
时 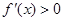
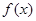 在[2,
在[2,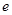 )上
)上
∴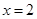 时
时 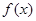 有极小值也就是最小值
有极小值也就是最小值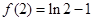
又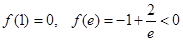
∴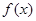 在[1,
在[1,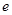 ]上最大值为
]上最大值为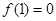
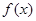 取值范围为[
取值范围为[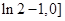
(2)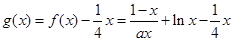
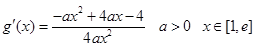
设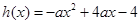 要使
要使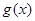 在[1,
在[1,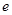 ]上 只须
]上 只须 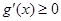
即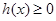 在[1,
在[1,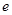 ]上恒成立
]上恒成立
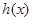 的对称轴为
的对称轴为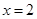 且开口向下
且开口向下
故只须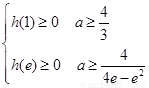
由此得出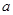 取值范围为
取值范围为 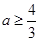
考点:导数的运用
点评:主要是考查了导数在研究函数单调性,以及极值和最值的运用,属于中档题。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
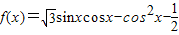
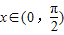 ,求f(x)的值域;
,求f(x)的值域;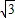 ,f(C)=0,若向量
,f(C)=0,若向量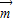 =(1,sinA)与向量
=(1,sinA)与向量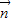 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.
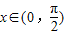 ,求f(x)的值域;
,求f(x)的值域; ,f(C)=0,若向量
,f(C)=0,若向量 =(1,sinA)与向量
=(1,sinA)与向量 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.
 的单调区间;
的单调区间; 的最小值;
的最小值; ,使得
,使得 的取值范围.
的取值范围.
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.