题目内容
已知函数
( I)当
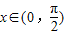 ,求f(x)的值域;
,求f(x)的值域;(II)设△ABC的内角A,B,C的对边分别为a,b,c,且c=
 ,f(C)=0,若向量
,f(C)=0,若向量 =(1,sinA)与向量
=(1,sinA)与向量 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.
【答案】分析:( I)化简函数f(x)的解析式为sin(2x-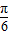 )-1,由
)-1,由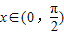 求得sin(2x-
求得sin(2x-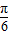 )的范围,可得函数的解析式.
)的范围,可得函数的解析式.
(II)△ABC中,由f(C)=sin(2C-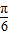 )-1=0求出sin(2C-
)-1=0求出sin(2C-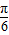 )的值,可得C=
)的值,可得C=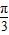 .再由两个向量共线的性质,可得b=2a,再由 cosC=
.再由两个向量共线的性质,可得b=2a,再由 cosC=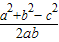 =
= ,求得a,b的值.
,求得a,b的值.
解答:解:( I)∵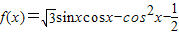 =
=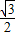 sin2x-
sin2x-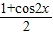 -
- =sin(2x-
=sin(2x-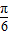 )-1,
)-1,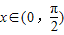 ,
,
∴2x-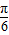 ∈(-
∈(- ,
,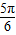 ),∴-
),∴- <sin(2x-
<sin(2x-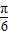 )≤1,∴-
)≤1,∴- <f(x)≤0,即函数f(x)的值域为(-
<f(x)≤0,即函数f(x)的值域为(- ,0].
,0].
(II)△ABC中,∵f(C)=sin(2C-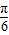 )-1=0,∴sin(2C-
)-1=0,∴sin(2C-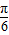 )=1,∴2C-
)=1,∴2C-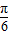 =
=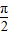 ,∴C=
,∴C=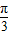 .
.
∵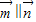 ,
,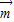 =(1,sinA)与向量
=(1,sinA)与向量 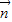 =(2,sinB),∴sinB-2sinA=0,由正弦定理可得 b=2a.
=(2,sinB),∴sinB-2sinA=0,由正弦定理可得 b=2a.
又 cosC=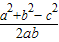 =
= ,解得a=1,b=2.
,解得a=1,b=2.
点评:本题主要考查三角函数的恒等变换及化简求值,余弦定理、两个向量共线的性质,正弦函数的定义域和值域,属于中档题.
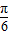 )-1,由
)-1,由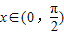 求得sin(2x-
求得sin(2x-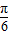 )的范围,可得函数的解析式.
)的范围,可得函数的解析式.(II)△ABC中,由f(C)=sin(2C-
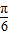 )-1=0求出sin(2C-
)-1=0求出sin(2C-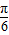 )的值,可得C=
)的值,可得C=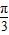 .再由两个向量共线的性质,可得b=2a,再由 cosC=
.再由两个向量共线的性质,可得b=2a,再由 cosC=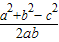 =
= ,求得a,b的值.
,求得a,b的值.解答:解:( I)∵
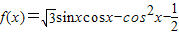 =
=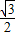 sin2x-
sin2x-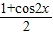 -
- =sin(2x-
=sin(2x-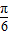 )-1,
)-1,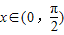 ,
,∴2x-
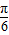 ∈(-
∈(- ,
,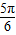 ),∴-
),∴- <sin(2x-
<sin(2x-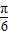 )≤1,∴-
)≤1,∴- <f(x)≤0,即函数f(x)的值域为(-
<f(x)≤0,即函数f(x)的值域为(- ,0].
,0].(II)△ABC中,∵f(C)=sin(2C-
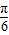 )-1=0,∴sin(2C-
)-1=0,∴sin(2C-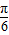 )=1,∴2C-
)=1,∴2C-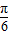 =
=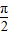 ,∴C=
,∴C=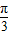 .
.∵
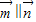 ,
,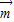 =(1,sinA)与向量
=(1,sinA)与向量 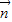 =(2,sinB),∴sinB-2sinA=0,由正弦定理可得 b=2a.
=(2,sinB),∴sinB-2sinA=0,由正弦定理可得 b=2a.又 cosC=
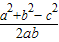 =
= ,解得a=1,b=2.
,解得a=1,b=2.点评:本题主要考查三角函数的恒等变换及化简求值,余弦定理、两个向量共线的性质,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
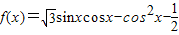
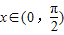 ,求f(x)的值域;
,求f(x)的值域;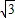 ,f(C)=0,若向量
,f(C)=0,若向量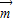 =(1,sinA)与向量
=(1,sinA)与向量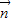 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.
 的单调区间;
的单调区间; 的最小值;
的最小值; ,使得
,使得 的取值范围.
的取值范围.
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.