题目内容
【必做题】解答时应写出文字说明、证明过程或演算步骤.
某射击运动员向一目标射击,该目标分为3个不同部分,第一、二、三部分面积之比为1:3:6.击中目标时,击中任何一部分的概率与其面积成正比.
(1)若射击4次,每次击中目标的概率为
且相互独立.设ξ表示目标被击中的次数,求ξ的分布列和数学期望E(ξ);
(2)若射击2次均击中目标,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求事件A发生的概率.
某射击运动员向一目标射击,该目标分为3个不同部分,第一、二、三部分面积之比为1:3:6.击中目标时,击中任何一部分的概率与其面积成正比.
(1)若射击4次,每次击中目标的概率为
| 1 | 3 |
(2)若射击2次均击中目标,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求事件A发生的概率.
分析:(1)依题意知ξ~B(4,
),由此能求出ξ的分布列和数学期望Eξ.
(2)设Ai表示事件“第一次击中目标时,击中第i部分”,i=1,2,Bi表示事件“第二次击中目标时,击中第i部分”,i=1,2.A=A1
∪
B1∪A1B1∪A2B2,由此能求出事件A发生的概率.
| 1 |
| 3 |
(2)设Ai表示事件“第一次击中目标时,击中第i部分”,i=1,2,Bi表示事件“第二次击中目标时,击中第i部分”,i=1,2.A=A1
. |
| B1 |
. |
| A1 |
解答:解:(1)依题意知ξ~B(4,
),ξ的分布列
数学期望Eξ=0×
+1×
+2×
+3×
+3×
+4×
=
.(或Eξ=np=
).…5分
(2)设Ai表示事件“第一次击中目标时,击中第i部分”,i=1,2,
Bi表示事件“第二次击中目标时,击中第i部分”,i=1,2.
依题意,知P(A1)=P(B1)=0.1,P(A2)=P(B2)=0.3,
A=A1
∪
B1∪A1B1∪A2B2,…7分
所求的概率为
P(A)=P(A1
)+P(
B1)+P(A1B1)+P(A2B2)
=P(A1)P(
)+P(
)P(B1)+P(A1)P(B1)+P(A2)P(B2)
=0.1×0.9+0.9×0.1+0.1×0.1+0.3×0.3
=0.28.
答:事件A发生的概率为0.28.…10分.
| 1 |
| 3 |
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 16 |
| 81 |
| 32 |
| 81 |
| 24 |
| 81 |
| 24 |
| 81 |
| 8 |
| 81 |
| 1 |
| 81 |
| 4 |
| 3 |
| 4 |
| 3 |
(2)设Ai表示事件“第一次击中目标时,击中第i部分”,i=1,2,
Bi表示事件“第二次击中目标时,击中第i部分”,i=1,2.
依题意,知P(A1)=P(B1)=0.1,P(A2)=P(B2)=0.3,
A=A1
. |
| B1 |
. |
| A1 |
所求的概率为
P(A)=P(A1
. |
| B1 |
. |
| A1 |
=P(A1)P(
. |
| B1 |
. |
| A1 |
=0.1×0.9+0.9×0.1+0.1×0.1+0.3×0.3
=0.28.
答:事件A发生的概率为0.28.…10分.
点评:本题考查离散型随机变量的数学期望和分布列的求法,解题时要认真审题,仔细解答,注意概率知识的合理运用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 中,
中,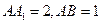 ,点
,点 是
是 的中点,点
的中点,点 在
在 上,设二面角
上,设二面角 的大小为
的大小为 。
。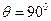 时,求
时,求 的长;
的长; 时,求
时,求 的长。
的长。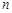 ,
,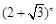 必可表示成
必可表示成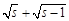 的形式,其中
的形式,其中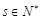 .
. ,从中任取一个.
,从中任取一个. ,至少存在另一个正整数
,至少存在另一个正整数 ,且
,且 ,使得
,使得 ”的概率;
”的概率; 为组成该数的相同数字的个数的最大值,求
为组成该数的相同数字的个数的最大值,求