��Ŀ����
���溯����ͼ�����ԭ�㣨����0��0�����Գ���һ���ʽ����ع㣬������Ľ��ۣ�
�ٺ���y=f��x������f��a+x��+f��a-x��=2b�ij�Ҫ������y=f��x����ͼ����ڵ㣨a��b�������ĶԳƣ�
�ں���y=f��x������F��x��=f��x+a��-f��a��Ϊ�溯���ij�Ҫ������y=f��x����ͼ����ڵ㣨a��f��a���������ĶԳƣ�ע����a������x�Ķ�����ʱ����f��a�������ڣ���
������������������и��⣺
��1��д������f��x��=tanx��ͼ��ĶԳ����ĵ����꣬������֤����
��2����֪m��m��-1��Ϊʵ�������ʺ���f(x)=
��ͼ���Ƿ����ijһ������ĶԳƣ����ǣ�����Գ����ĵ����겢˵�����ɣ������ǣ���˵�����ɣ�
��3��������f(x)=(x-
)(|x+t|+|x-3|)-4��ͼ����ڵ�(
��f(
))�����ĶԳƣ���t��ֵ��
�ٺ���y=f��x������f��a+x��+f��a-x��=2b�ij�Ҫ������y=f��x����ͼ����ڵ㣨a��b�������ĶԳƣ�
�ں���y=f��x������F��x��=f��x+a��-f��a��Ϊ�溯���ij�Ҫ������y=f��x����ͼ����ڵ㣨a��f��a���������ĶԳƣ�ע����a������x�Ķ�����ʱ����f��a�������ڣ���
������������������и��⣺
��1��д������f��x��=tanx��ͼ��ĶԳ����ĵ����꣬������֤����
��2����֪m��m��-1��Ϊʵ�������ʺ���f(x)=
| x+m |
| x-1 |
��3��������f(x)=(x-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
��1������f��x��=tanx��ͼ��ĶԳ����ĵ�����Ϊ(
��0)��k��N*���� ����2�֣�
��k=2n��n��N*��ʱ��tan(
+x)+tan(
-x)=tanx-tanx=0��
��k=2n+1��n��N*��ʱ��tan(
+x)+tan(
-x)=-cotx+cotx=0����֤�� ����6�֣�
��2����f(x)=
=1+
����f��x����ͼ��ĶԳ����ĵ�����Ϊ��1��1��������9�֣�f(x+1)+f(1-x)=
+
=
+
=2���ɽ��ۢٵã���ʵ��m��m��-1��������f(x)=
��ͼ����ڵ㣨1��1�������ĶԳƣ� ����12�֣�
��3���ɽ��ۢ�F(x)=f(x+
)-f(
)=x(|x+
+t|+|x-
|)Ϊ�溯��������14�֣�
����g��x��=xΪ�溯������h(x)=|x+
+t|+|x-
|Ϊż����
���ǣ���h��x��=h��-x���ɵ�|x+
+t|+|x-
|=|x-(
+t)|+|x+
|������16�֣�
��ˣ�
+t=
�����t=
Ϊ���� ����18�֣�
| k�� |
| 2 |
��k=2n��n��N*��ʱ��tan(
| k�� |
| 2 |
| k�� |
| 2 |
��k=2n+1��n��N*��ʱ��tan(
| k�� |
| 2 |
| k�� |
| 2 |
��2����f(x)=
| x+m |
| x-1 |
| m+1 |
| x-1 |
| x+1+m |
| x+1-1 |
| 1-x+m |
| 1-x-1 |
| x+1+m |
| x |
| -x+1+m |
| -x |
| x+m |
| x-1 |
��3���ɽ��ۢ�F(x)=f(x+
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
����g��x��=xΪ�溯������h(x)=|x+
| 2 |
| 3 |
| 7 |
| 3 |
���ǣ���h��x��=h��-x���ɵ�|x+
| 2 |
| 3 |
| 7 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
��ˣ�
| 2 |
| 3 |
| 7 |
| 3 |
| 5 |
| 3 |

��ϰ��ϵ�д�
 �żӾ���ϵ�д�
�żӾ���ϵ�д�
�����Ŀ
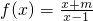 ��ͼ���Ƿ����ijһ������ĶԳƣ����ǣ�����Գ����ĵ����겢˵�����ɣ������ǣ���˵�����ɣ�
��ͼ���Ƿ����ijһ������ĶԳƣ����ǣ�����Գ����ĵ����겢˵�����ɣ������ǣ���˵�����ɣ�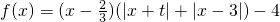 ��ͼ����ڵ�
��ͼ����ڵ�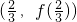 �����ĶԳƣ���t��ֵ��
�����ĶԳƣ���t��ֵ��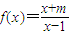 ��ͼ���Ƿ����ijһ������ĶԳƣ����ǣ�����Գ����ĵ����겢˵�����ɣ������ǣ���˵�����ɣ�
��ͼ���Ƿ����ijһ������ĶԳƣ����ǣ�����Գ����ĵ����겢˵�����ɣ������ǣ���˵�����ɣ�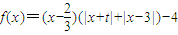 ��ͼ����ڵ�
��ͼ����ڵ�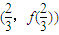 �����ĶԳƣ���t��ֵ��
�����ĶԳƣ���t��ֵ��