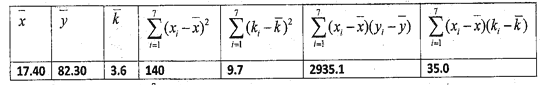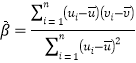题目内容
【题目】对于给定的正整数![]() ,若数列
,若数列![]() 满足
满足![]() 对任意正整数
对任意正整数![]() 总成立,则称数列
总成立,则称数列![]() 是“
是“![]() 数列”.
数列”.
(1)证明:等差数列![]() 是“
是“![]() 数列”;
数列”;
(2)若数列![]() 既是“
既是“![]() 数列”,又是“
数列”,又是“![]() 数列”,证明:
数列”,证明: ![]() 是等差数列.
是等差数列.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)因为![]() 是等差数列,设其公差为
是等差数列,设其公差为![]() ,则
,则![]() ,只需证明
,只需证明![]() ,即可得到等差数列
,即可得到等差数列![]() 是“
是“![]() 数列”;(2)数列
数列”;(2)数列![]() 既是“
既是“![]() 数列”,又是“
数列”,又是“![]() 数列”,可得,
数列”,可得, ![]() ,结合两式化为
,结合两式化为![]() ,其中
,其中![]() ,验证前四项也是等差数列即可得结论.
,验证前四项也是等差数列即可得结论.
试题解析: (1)因为![]() 是等差数列,设其公差为
是等差数列,设其公差为![]() ,
,
则![]() ,从而,当
,从而,当![]() 时,
时, ![]()
![]()
所以an-3+an-2+an-1+an+1+an+2+an+3=6an,
因此等差数列{an}是“P(3)数列”.
(2)数列{an}既是“P(2)数列”,又是“P(3)数列”,因此,
当n≥3时,an-2+an-1+an+1+an+2=4an,①
当n≥4时,an-3+an-2+an-1+an+1+an+2+an+3=6an.②
由①知,an-3+an-2=4an-1-(an+an+1),③
an+2+an+3=4an+1-(an-1+an).④
将③④代入②,得an-1+an+1=2an,其中n≥4,
所以a3,a4,a5,…是等差数列,设其公差为d′.
在①中,取n=4,则a2+a3+a5+a6=4a4,
所以a2=a3-d′,
在①中,取n=3,则a1+a2+a4+a5=4a3,
所以a1=a3-2d′,
所以数列{an}是等差数列.

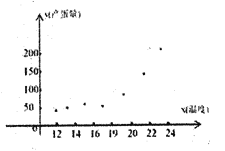
【题目】某研究性学习小组对昼夜温差大小与某种子发芽多少之间的关系进行研究,下面是3月1日至5日每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数的详细记录:
(1)根据3月2日至3月4日的数据,用最小二乘法求出y关于x的线性回归方程;
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均小于2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
参考公式: ,
,![]() .
.