题目内容
已知二次函数f(x)=ax2+bx,且f(x+1)为偶函数,定义:满足f(x)=x的实数x称为函数f(x)的不动点,若函数f(x)有且仅有一个不动点,
(1)求f(x)的解析式;
(2) 若函数g(x)= f(x)+![]() +
+![]() x2在 (0,
x2在 (0,![]() ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;
(3)在(2)的条件下,是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由。
(1)f(x)= -![]() x2+x;(2)k
x2+x;(2)k![]()
![]() ;(3)同解析。
;(3)同解析。
解析:
(1)f(x+1) =a(x+1) 2+b(x+1) = ax 2+(2a+b)x+a+b为偶函数,
∴2a+b=0,∴b=-2a,∴f(x)=ax2-2ax,′
∵函数f(x)有且仅有一个不动点,∴方程f(x)=x有且仅有一个解,
∴ax2-(2a+1)x=0有且仅有一个解,∴2a+1=0,a=-![]() ,∴f(x)= -
,∴f(x)= -![]() x2+x
x2+x
(2) g(x)= f(x)+![]() +
+![]() x2=x+
x2=x+![]() 在 (0,
在 (0,![]() ]上是单调增函数,
]上是单调增函数,
当k![]() 0时,g(x)= x+
0时,g(x)= x+![]() 在(0,+
在(0,+![]() )上是单调增函数,∴不成立;′
)上是单调增函数,∴不成立;′
当k>0时,g(x)= x+![]() 在(0,
在(0,![]() ]上是单调减函数,∴
]上是单调减函数,∴![]()
![]()
![]() ,∴k
,∴k![]()
![]()
(3)∵f(x)= -![]() x2+x= -
x2+x= -![]() (x-1)2+
(x-1)2+![]()
![]()
![]() ,∴kn
,∴kn![]()
![]() ,∴n
,∴n![]()
![]()
![]()
![]() <1,
<1,
∴f(x)在区间[m,n]上是单调增函数
∴![]() ,即
,即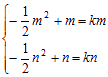 ,方程
,方程![]() 的两根为0,2-2k′
的两根为0,2-2k′
当2-2k>0,即![]()
![]() k<1时,[m,n]= [0,2-2k]
k<1时,[m,n]= [0,2-2k]
当2-2k<0,即k>1时,[m,n]= [2-2k,0]′
当2-2k=0,即k=1时,[m,n] 不存在′

练习册系列答案
相关题目