题目内容
已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且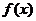 在
在 处取得极小值
处取得极小值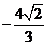 。设
。设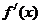 表示
表示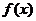 的导函数,定义数列
的导函数,定义数列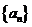 满足:
满足:

(Ⅰ)求数列 的通项公式
的通项公式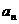 ;
;
(Ⅱ)对任意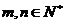 ,若
,若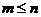 ,证明:
,证明: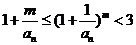 ;
;
(Ⅲ)(理科)试比较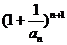 与
与 的大小。
的大小。
【答案】
解:(Ⅰ)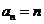
(Ⅱ)由(Ⅰ)知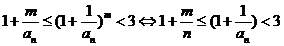 。因为
。因为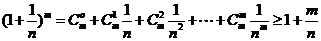 (当
(当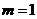 时取等号)。又
时取等号)。又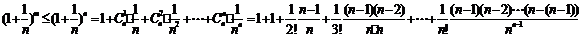
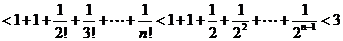
(Ⅲ)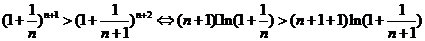 ,构造函数
,构造函数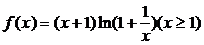 ,则上式等价于证
,则上式等价于证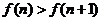 成立,所以
成立,所以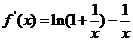 。又令
。又令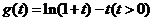 ,则
,则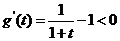 当
当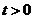 时成立,即得
时成立,即得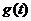 在
在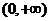 上单调递减,于是
上单调递减,于是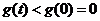 成立,即
成立,即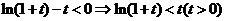 成立,故
成立,故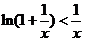 成立。所以
成立。所以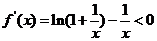 ,由此知
,由此知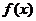 单调递减,所以
单调递减,所以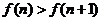 ,即
,即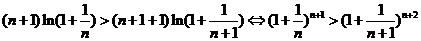 ,所以
,所以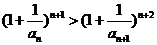

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若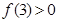 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;