题目内容
11.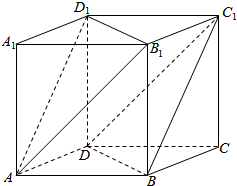 如图所示,已知多面体ABCD-A1B1C1D1是棱长为1的正方体.
如图所示,已知多面体ABCD-A1B1C1D1是棱长为1的正方体.(1)求证:平面AB1D1∥平面BDC1;
(2)求四棱锥D1-AB1C1D的体积.
分析 (1)在平面AB1D1找两条相交直线AB1,AD1分别平行于平面BDC1;
(2)连接D1C,设D1C∩C1D=O,证明D1O为四棱锥D1-AB1C1D的高,求出底面积,即可求四棱锥D1-AB1C1D的体积.
解答  (1)证明:由已知,在四边形DBB1D1中,BB1∥DD1且BB1=DD1,
(1)证明:由已知,在四边形DBB1D1中,BB1∥DD1且BB1=DD1,
故四边形DBB1D1为平行四边形,即D1B1∥DB,-----2’
∵D1B1?平面DBC1,∴D1B1∥平面DBC1;-----3’
同理在四边形ADC1B1中,AB1∥DC1,-----4’
同理AB1∥平面DBC1,-------5’
又∵AB1∩D1B1=B1,-----6’
∴平面AB1D1∥平面BDC1.----7’
(2)解:连接D1C,设D1C∩C1D=O,
则在正方形D1CICD中,D1C⊥DC1,----8’
又在正方体ABCD-A1B1C1D1中,B1C1⊥平面C1CDD1,
所以D1C⊥B1C1,----9’
∵DC1∩B1C1=C1,∴D1C⊥平面AB1C1D,--10’
即D1O为四棱锥D1-AB1C1D的高;
由已知,在正方形DCC1D1中,边长为1,
∴D1C=DC1=$\sqrt{2}$,∴四棱锥的高D1O=$\frac{\sqrt{2}}{2}$,----11’
又在正方体ABCD-A1B1C1D1中,四边形AB1C1D为矩形,且C1D=$\sqrt{2}$,B1C1=1,
故${S}_{A{B}_{1}{C}_{1}D}$=1×$\sqrt{2}$=$\sqrt{2}$----12’
∴${V}_{D-A{B}_{1}{C}_{1}D}$=$\frac{1}{3}×\frac{\sqrt{2}}{2}×\sqrt{2}$=$\frac{1}{3}$----14’
点评 本题考查平面与平面平行的判定,考查四棱锥D1-AB1C1D的体积,考查学生分析解决问题的能力,属于中档题.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
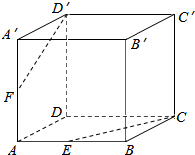
| A. | 都与直线DA相交,且交于同一点 | B. | 互相平行 | ||
| C. | 异面 | D. | 都与直线DA相交,但交于不同点 |
| A. | 8 | B. | 2 | C. | 16 | D. | 3 |
| A. | $\frac{1}{8}$ | B. | $\frac{3}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{27}{64}$ |