题目内容
(文)我国是世界上严重缺水的国家之一,城市缺水问题较为突出。某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准。为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况。现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如下图表:
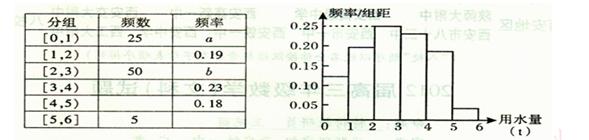
(1)分别求出n,a,b的值;
(2)若从样本中月均用水量在[5,6](单位:t)的5位居民中任选2人作进一步的调查研究,求月均用水量最多的居民被选中的频率(5位居民的月均用水量均不相等。)

(1)分别求出n,a,b的值;
(2)若从样本中月均用水量在[5,6](单位:t)的5位居民中任选2人作进一步的调查研究,求月均用水量最多的居民被选中的频率(5位居民的月均用水量均不相等。)
(1)0.125;(2) .
.
 .
.本试题主要考查了频率分布直方图的运用。利用由频率分布直方图得月均用水量在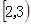 的频率为0.25,即
的频率为0.25,即 ….. 2分
….. 2分
又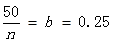

第二问中,记样本中月均用水量在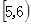 (单位:t)的5位居民为
(单位:t)的5位居民为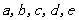 ,且不妨设
,且不妨设 为月均用水量最多的居民,记月均用水量最多的居民被选中为事件A,所以基本事件为:
为月均用水量最多的居民,记月均用水量最多的居民被选中为事件A,所以基本事件为: ,
, ,
, ,
, ,
, ,
, ,
, ,
, 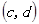 ,
, ,
, 共10个,
共10个,
而事件A包含的基本事件有 ,
, ,
, ,
, 共4个,这样可以利用古典概型求解概率。
共4个,这样可以利用古典概型求解概率。
解:(1) 由频率分布直方图得月均用水量在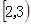 的频率为0.25,即
的频率为0.25,即 ….. 2分
….. 2分
又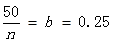 …………………………………………….. 4分
…………………………………………….. 4分
 ………………………………. 6分
………………………………. 6分
(2).记样本中月均用水量在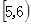 (单位:t)的5位居民为
(单位:t)的5位居民为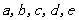 ,且不妨设
,且不妨设 为月均用水量最多的居民,记月均用水量最多的居民被选中为事件A,所以基本事件为:
为月均用水量最多的居民,记月均用水量最多的居民被选中为事件A,所以基本事件为: ,
, ,
, ,
, ,
, ,
, ,
, ,
, 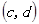 ,
, ,
, 共10个,
共10个,
而事件A包含的基本事件有 ,
, ,
, ,
, 共4个。……………. 10分
共4个。……………. 10分
所以月均用水量最多的居民被选中的概率 =
= ……… 12分
……… 12分
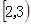 的频率为0.25,即
的频率为0.25,即 ….. 2分
….. 2分又
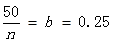

第二问中,记样本中月均用水量在
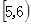 (单位:t)的5位居民为
(单位:t)的5位居民为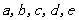 ,且不妨设
,且不妨设 为月均用水量最多的居民,记月均用水量最多的居民被选中为事件A,所以基本事件为:
为月均用水量最多的居民,记月均用水量最多的居民被选中为事件A,所以基本事件为: ,
, ,
, ,
, ,
, ,
, ,
, ,
, 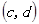 ,
, ,
, 共10个,
共10个,而事件A包含的基本事件有
 ,
, ,
, ,
, 共4个,这样可以利用古典概型求解概率。
共4个,这样可以利用古典概型求解概率。解:(1) 由频率分布直方图得月均用水量在
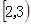 的频率为0.25,即
的频率为0.25,即 ….. 2分
….. 2分又
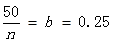 …………………………………………….. 4分
…………………………………………….. 4分 ………………………………. 6分
………………………………. 6分(2).记样本中月均用水量在
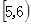 (单位:t)的5位居民为
(单位:t)的5位居民为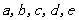 ,且不妨设
,且不妨设 为月均用水量最多的居民,记月均用水量最多的居民被选中为事件A,所以基本事件为:
为月均用水量最多的居民,记月均用水量最多的居民被选中为事件A,所以基本事件为: ,
, ,
, ,
, ,
, ,
, ,
, ,
, 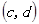 ,
, ,
, 共10个,
共10个,而事件A包含的基本事件有
 ,
, ,
, ,
, 共4个。……………. 10分
共4个。……………. 10分所以月均用水量最多的居民被选中的概率
 =
= ……… 12分
……… 12分
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 (含80)以上时,属醉酒驾车。属醉酒驾车。据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共100
(含80)以上时,属醉酒驾车。属醉酒驾车。据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共100
 【解】 频率分布表 频率分布直方图
【解】 频率分布表 频率分布直方图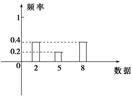
 ;
; ;
;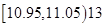 ;
; ;
; ;
; ;
; ;
;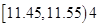 ;
; ;
; 范围内的可能性是百分之几?
范围内的可能性是百分之几? 中,其频率分布直方图如图所示,由图中数据可知
中,其频率分布直方图如图所示,由图中数据可知 ,在抽测的100根中,棉花纤维的长度在
,在抽测的100根中,棉花纤维的长度在 内的有 根。
内的有 根。
