题目内容
函数f(x)=x2+bx的图象在点A(1,f(1))处的切线与直线3x-y+2=0平行,若数列{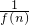 }的前n项和为Sn,则S2012的值为
}的前n项和为Sn,则S2012的值为
- A.

- B.

- C.

- D.
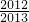
D
分析:对函数求导,根据导数的几何意义可求切线在x=1处的斜率,然后根据直线平行时斜率相等的条件可求b,代入可求f(n),利用裂项求和即可求
解答:∵f(x)=x2+bx
∴f′(x)=2x+b
∴y=f(x)的图象在点A(1,f(1))处的切线斜率k=f′(1)=2+b
∵切线与直线3x-y+2=0平行
∴b+2=3
∴b=1,f(x)=x2+x
∴f(n)=n2+n=n(n+1)
∴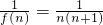 =
=
∴S2012=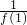
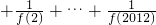
=1-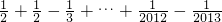
=1- =
=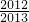
故选D
点评:本题以函数的导数的几何意义为载体,主要考查了切线斜率的求解,两直线平行时的斜率关系的应用,及裂项求和方法的应用.
分析:对函数求导,根据导数的几何意义可求切线在x=1处的斜率,然后根据直线平行时斜率相等的条件可求b,代入可求f(n),利用裂项求和即可求
解答:∵f(x)=x2+bx
∴f′(x)=2x+b
∴y=f(x)的图象在点A(1,f(1))处的切线斜率k=f′(1)=2+b
∵切线与直线3x-y+2=0平行
∴b+2=3
∴b=1,f(x)=x2+x
∴f(n)=n2+n=n(n+1)
∴
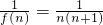 =
=
∴S2012=
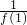
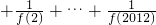
=1-
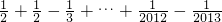
=1-
 =
=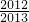
故选D
点评:本题以函数的导数的几何意义为载体,主要考查了切线斜率的求解,两直线平行时的斜率关系的应用,及裂项求和方法的应用.

练习册系列答案
相关题目