Question

【题目】如图，已知长方形ABCD中，，，M为DC的中点，将沿AM折起，使得平面平面ABCM．

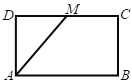
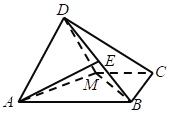
（1）求证：平面平面BMD；

（2）若点E是线段DB上的一动点，问为何值时，二面角的余弦值为．

Answer 1

【答案】（1）证明见解析；（2）的值为.

【解析】

（1）首先证明线面垂直，利用线面垂直证明面面垂直；

（2）建立空间直角坐标系，列出各点坐标，求出平面法向量，根据面面角的公式以及二面角的余弦值可求出.

（1）长方形ABCD中，，，M为DC的中点，

，

故，所以，

平面平面ABCM，平面平面，平面ABCM，

平面ADM，

平面BDM，

平面平面BMD；

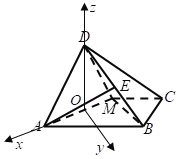
（2）建立如图所示的直角坐标系，则平面ADM的一个法向量，

设，则，

又，，，，

故，

，，

，

设平面AME的一个法向量为，

则，即，取，

由题意知，

故，

即，解得，

故当的值为时，二面角的余弦值为．