题目内容
(本小题满分15分)
在等比数列{an}中,首项为 ,公比为
,公比为 ,
, 表示其前n项和.
表示其前n项和.
(I)记 =A,
=A, = B,
= B, = C,证明A,B,C成等比数列;
= C,证明A,B,C成等比数列;
(II)若 ,
, ,记数列
,记数列 的前n项和为
的前n项和为 ,当n取何值时,
,当n取何值时, 有最小值.
有最小值.
【答案】
解:(I)当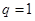 时,
时,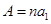 ,
,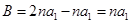 ,
,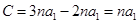 ,可见A,B,C成等比数列;
————2分
,可见A,B,C成等比数列;
————2分
当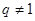 时,
时,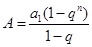 ,
,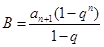 ,
,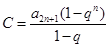 .
.
故有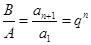 ,
,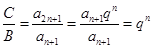 .可得
.可得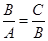 ,这说明A,B,C成等比数列.
,这说明A,B,C成等比数列.
综上,A,B,C成等比数列. ————7分
(II)若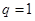 ,则
,则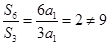 ,与题设矛盾,此情况不存在;
,与题设矛盾,此情况不存在;
若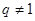 ,则
,则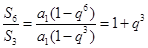 ,故有
,故有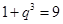 ,解得
,解得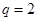 .——9分
.——9分
所以 ,可知
,可知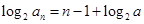 .所以数列
.所以数列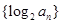 是以
是以 为首项,1为公差的等差数列.
为首项,1为公差的等差数列.
令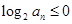 ,即
,即 .
.
因为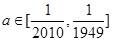 ,所以
,所以 ,——12分
,——12分
即得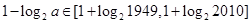 ,
,
可知满足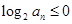 的最大的n值为11.
的最大的n值为11.
所以,数列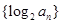 的前11项均为负值,从第12项开始都是正数.因此,当
的前11项均为负值,从第12项开始都是正数.因此,当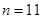 时,
时,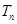 有最小值. ————15分
有最小值. ————15分
【解析】略

练习册系列答案
相关题目

 的单调区间;
的单调区间; ,试分别解答以下两小题.
,试分别解答以下两小题. 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
. 、
、 分别为椭圆
分别为椭圆 :
: 的
的  :
: 的焦点,
的焦点, 是
是 。
。 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由; 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.