题目内容
..(本小题满分12分)
数列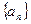 的各项均为正数,
的各项均为正数,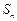 为其前
为其前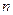 项和,对于任意
项和,对于任意 ,总有
,总有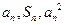 成等差数列.
成等差数列.
(1)求数列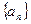 的通项公式;
的通项公式;
(2)设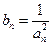 ,数列
,数列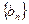 的前
的前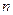 项和为
项和为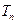 ,求证:
,求证: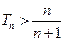 .
.
解:(1)由已知:对于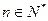 ,总有
,总有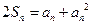 ①成立
①成立
∴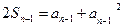 (n ≥ 2)②
(n ≥ 2)②
①-②得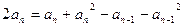
∴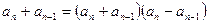
∵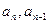 均为正数,∴
均为正数,∴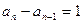 (n ≥ 2)
(n ≥ 2)
∴数列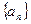 是公差为1的等差数列
是公差为1的等差数列
又n=1时,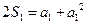 , 解得
, 解得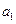 ="1, "
="1, "
∴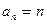 .(
.(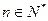 )
)
(2) 解:由(1)可知 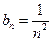
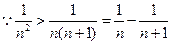
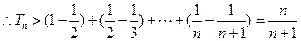
解析

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 内的随机点,求函数
内的随机点,求函数