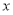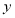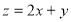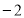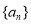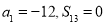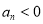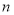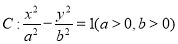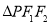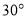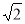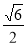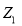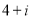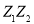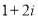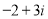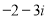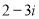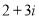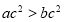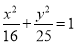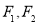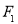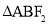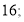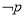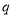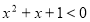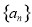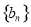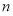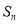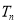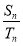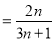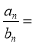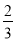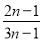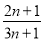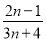题目内容
已知椭圆 、抛物线
、抛物线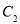 的焦点均在
的焦点均在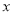 轴上,
轴上, 的中心和
的中心和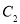 的顶点均为原点
的顶点均为原点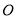 ,从每条曲线上取两个点,将其坐标记录如下:
,从每条曲线上取两个点,将其坐标记录如下: 、
、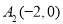 、
、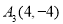 、
、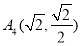 .
.
(1)经判断点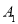 ,
,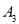 在抛物线
在抛物线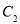 上,试求出
上,试求出 的标准方程;
的标准方程;
(2)求抛物线 的焦点
的焦点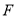 的坐标并求出椭圆
的坐标并求出椭圆 的离心率;
的离心率;
(3)过 的焦点
的焦点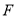 直线与椭圆
直线与椭圆 交不同两点
交不同两点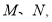 且满足
且满足 ,试求出直线的方程.
,试求出直线的方程.
(1)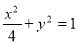 ;(2)
;(2)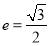 ;(3)
;(3)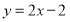 或
或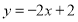 .
.
【解析】
试题分析:(1)先设抛物线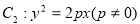 ,然后将
,然后将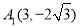 或
或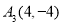 代入可得
代入可得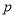 ,从而确定了
,从而确定了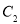 的方程,也进一步确定
的方程,也进一步确定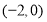 、
、 不在
不在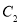 上,只能在
上,只能在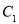 上;设
上;设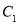 :
: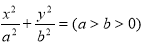 ,把点
,把点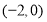 、
、 代入得
代入得 ,求解即可确定
,求解即可确定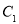 的方程;(2)由(1)中所求得的方程不难得到
的方程;(2)由(1)中所求得的方程不难得到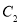 的焦点
的焦点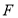 及椭圆
及椭圆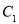 的离心率
的离心率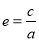 ;(3)先假设所求直线的方程
;(3)先假设所求直线的方程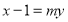 (或
(或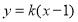 ,不过此时要先验证直线斜率不存在的情况),然后联立直线与椭圆的方程,消去消去
,不过此时要先验证直线斜率不存在的情况),然后联立直线与椭圆的方程,消去消去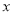 ,得
,得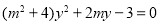 ,得到
,得到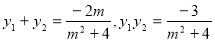 ,再得到
,再得到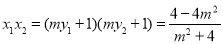 ,要使
,要使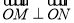 ,只须
,只须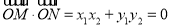 ,从中求解即可得到
,从中求解即可得到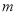 ,从而可确定直线的方程.
,从而可确定直线的方程.
试题解析:(1)设抛物线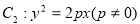 ,则有
,则有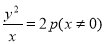 ,而
,而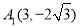 、
、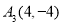 在抛物线上 2分
在抛物线上 2分
将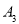 坐标代入曲线方程,得
坐标代入曲线方程,得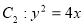 3分
3分
设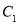 :
: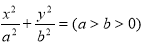 ,把点
,把点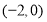 、
、 代入得
代入得
 解得
解得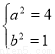
∴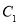 方程为
方程为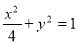 6分
6分
(2)显然,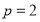 ,所以抛物线焦点坐标为
,所以抛物线焦点坐标为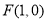
由(1)知,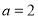 ,
,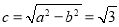
所以椭圆的离心率为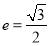 8分
8分
(3)法一:直线过抛物线焦点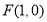 ,设直线的方程为
,设直线的方程为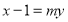 ,两交点坐标为
,两交点坐标为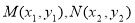 ,
,
由 消去
消去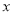 ,得
,得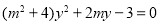 10分
10分
∴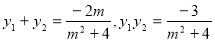 ①
①
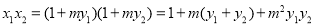
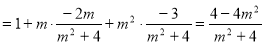 ② 12分
② 12分
由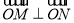 ,即
,即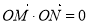 ,得
,得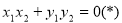
将①②代入(*)式,得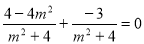 ,解得
,解得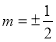 14分
14分
所求的方程为: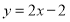 或
或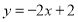 15分
15分
法二:容易验证直线的斜率不存在时,不满足题意 9分
当直线斜率存在时,直线过抛物线焦点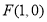 ,设其方程为
,设其方程为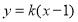 ,与
,与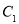 的交点坐标为
的交点坐标为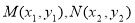
由 消掉
消掉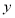 ,得
,得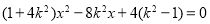 , 10分
, 10分
于是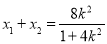 ,
,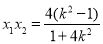 ①
①
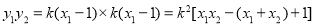
即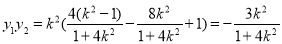 ② 12分
② 12分
由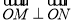 ,即
,即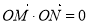 ,得
,得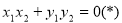
将①、②代入(*)式,得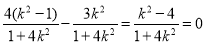
解得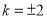 14分
14分
故所求的方程为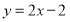 或
或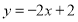 15分.
15分.
考点:1.抛物线的标准方程及其几何性质;2.椭圆的标准方程及其几何性质;3.直线与圆锥曲线的综合问题.