题目内容
已知函数f(x)=x3-3x2+2b,满足:f(1+x)+f(1-x)=2b,且方程f(x)-2t=0在区间[-1,t](t>-1)上只有一个解,则实数t的取值范围是( )
分析:由于f(1+x)+f(1-x)=2b,代入函数解析式得出b值,从而得出函数f(x)的解析式,又f(x)-2t=0?f(x)=2t,设y=f(x),y=2t,画出这两个函数的图象,如图所示.下面结合图象就t的取值进行分类讨论,即可得到实数t的取值范围.
解答: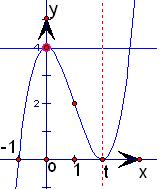
 解:由于f(1+x)+f(1-x)=2b,
解:由于f(1+x)+f(1-x)=2b,
∴(x+1)3-3(x+1)2+2b+(1-x)3-3(1-x)2+2b=2b
⇒b=2.
∴f(x)=x3-3x2+4,
又f(x)-2t=0?f(x)=2t,设y=f(x),y=2t,
画出这两个函数的图象,如图所示.
在方程f(x)-2t=0中令x=t得:t3-3t2+4-2t=0,
⇒(t-1)(t2-2t-4)=0⇒t=1或t=1±
,
①当t∈[0,1]时,它们在区间[-1,t](t>-1)上只有一个交点;
②当t=2时,它们在区间[-1,t](t>-1)上只有一个交点;
③当t∈[1+
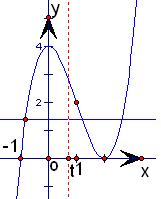
,+∞)时,它们在区间[-1,t](t>-1)上只有一个交点;如图.
综上所述,则实数t的取值范围是(-
,1)∪[
,+∞)∪{2}.
故选A.

 解:由于f(1+x)+f(1-x)=2b,
解:由于f(1+x)+f(1-x)=2b,∴(x+1)3-3(x+1)2+2b+(1-x)3-3(1-x)2+2b=2b
⇒b=2.
∴f(x)=x3-3x2+4,
又f(x)-2t=0?f(x)=2t,设y=f(x),y=2t,
画出这两个函数的图象,如图所示.
在方程f(x)-2t=0中令x=t得:t3-3t2+4-2t=0,
⇒(t-1)(t2-2t-4)=0⇒t=1或t=1±
| 5 |
①当t∈[0,1]时,它们在区间[-1,t](t>-1)上只有一个交点;
②当t=2时,它们在区间[-1,t](t>-1)上只有一个交点;

③当t∈[1+
| 5 |
综上所述,则实数t的取值范围是(-
| 1 |
| 2 |
| 7 |
| 2 |
故选A.
点评:本小题主要考查函数单调性的应用、根的存在性及根的个数判断、方程的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|