题目内容
已知p:二次函数f(x)=x2-7x+6在区间[m,+∞)是增函数; q:二次不等式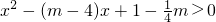 的解集为R.若p∨q为真,p∧q为假,求实数m的取值范围.
的解集为R.若p∨q为真,p∧q为假,求实数m的取值范围.
解:对于p:因为二次函数f(x)=x2-7x+6的对称轴为x= ,由题意知m≥
,由题意知m≥ ,
,
即若p真,则m∈[ ,+∞);
,+∞);
对于q:由△=(m-4)2-4(1- m)=m2-7m+12<0,
m)=m2-7m+12<0,
解得3<m<4,
即若q真,则m∈(3,4).
由题意知:p,q一真一假,
若p真q假,则m∈[4,+∞);
若p假q真,则m∈(3, );
);
综合得实数m的取值范围为∈(3, )∪[4,+∞);
)∪[4,+∞);
分析:若p真,可求得m的取值范围;若q真同理得m的取值范围;利用真值表计算即可求得答案.
点评:本题考查命题的真假判断与应用,着重考查二次函数的单调性与恒成立问题,考查真值表的应用及解不等式组的能力,属于中档题.
 ,由题意知m≥
,由题意知m≥ ,
,即若p真,则m∈[
 ,+∞);
,+∞);对于q:由△=(m-4)2-4(1-
 m)=m2-7m+12<0,
m)=m2-7m+12<0,解得3<m<4,
即若q真,则m∈(3,4).
由题意知:p,q一真一假,
若p真q假,则m∈[4,+∞);
若p假q真,则m∈(3,
 );
);综合得实数m的取值范围为∈(3,
 )∪[4,+∞);
)∪[4,+∞);分析:若p真,可求得m的取值范围;若q真同理得m的取值范围;利用真值表计算即可求得答案.
点评:本题考查命题的真假判断与应用,着重考查二次函数的单调性与恒成立问题,考查真值表的应用及解不等式组的能力,属于中档题.

练习册系列答案
相关题目